This blog tells you how to build a transformers from scratch.
Why when need transformers
How far the Neural Network can look back depends on the length of the NN and the choice.
CNN have a notable disadvantage for time series prediction :
- Increase the kernel size(also increase the parameters).
Skips oversome past state/inputs
$\rightarrow$ trade-off
Transformers
Attention
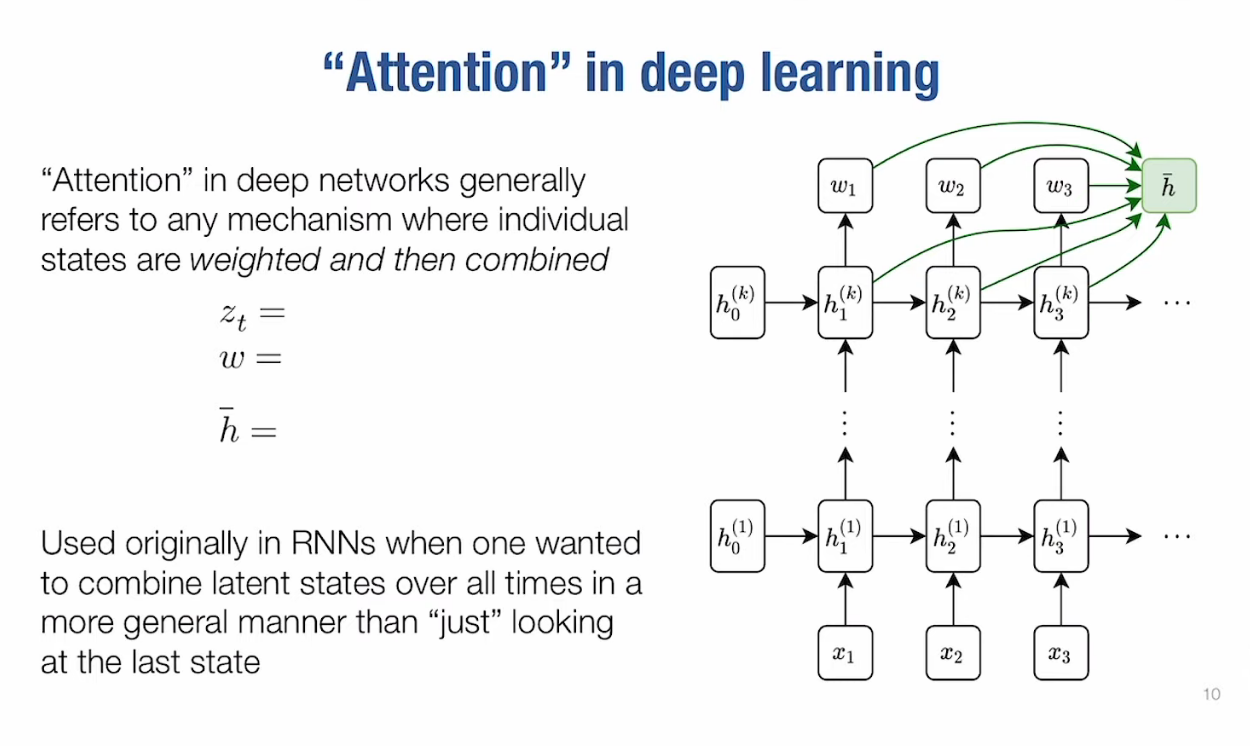
Attention in deep networks generally refers to any mechanism
where individual states are weighted and then combined.
The states depend more on the later element than the previous element (problem for RNN, LSTM).
For the
Attention, we take several latter states rather than one to compute :
$$
\overline{h} = \sum_{t=1}^T w_th_t(k) \text{for example the whole time sequence}
$$
Self-Attention Mechansim
$K,Q,V\in R^{T\times d}$ (keys, queries, values):
To get $K$, $K = XW_k$, $k_1$ only depends on the $x_1$, and so on.
$$
SelfAttention(K,Q,V) = softmax(\frac{KQ^T}{\sqrt{d}}) V
$$
$KQ^T$ is $R ^{T\times T}$ , in this matrix:
$$
entry_{(i,j)} = k_i^Tq_j
$$
Similarity of the $k_i$ and $q_j$.The softmax is by row, each of the row will now turn into weights sum to 1.
$d\in R^{T\times}$, so the output is also $R^{T\times d}$.
Each row of the output
Properties:
- Invariant, same permutations of the $K,Q,V$ lead to the same permutation of the output.
- Allows influence between $k_t, q_t, v_t$ over all times. Without increase the parameter counts
- Compute cost is $O(T^2 d +Td)$.
Transformers architecture

Transformer Block
$z_1 = SelfAttention(z^{i}w_K,z^{i}w_Q,z^{i}w_V = softmax(\frac{z^{i}w_Kw_Q^Tz^{i T}}{\sqrt{d}}) z^{i}w_V$
$z_2 = LayerNorm(z^{i}+z_1)$
$z^{i+1} = LayerNorm(z_2+Relu(z_2w_1)w_2)$
$Relu(z_2w_1)w_2$ is a two layer network in the MLP.
Masked Self-Attention
Encode the position into the transformer

After the softmax, make the upper triangle are all zeros.
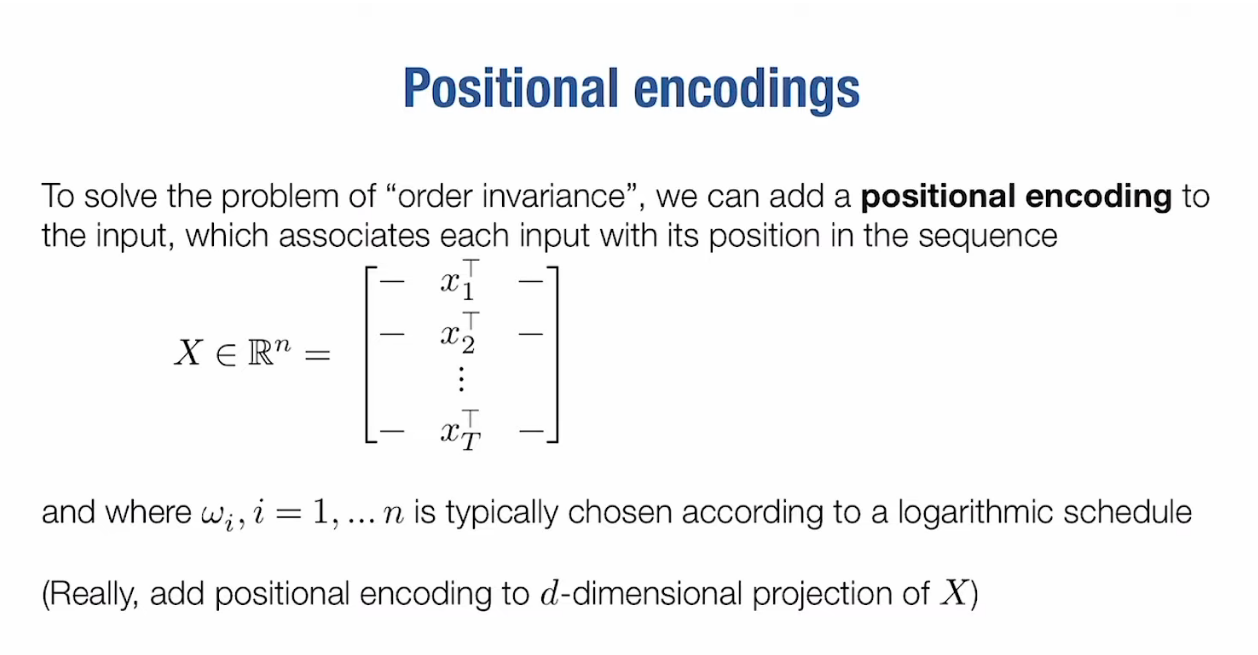

Add Position encoding so that the neural network knows where is the x.
