DeePMD 调研报告
简介
背景介绍
分子动力学(MD)模拟在凝聚态物理、材料科学、聚合物化学和分子生物学等领域具有广泛的应用,它允许研究人员检查原子或分子的行为,这在实验难以进行时尤为宝贵。然而,MD模拟的质量受到势能(PES)准确性的限制。传统上,有两种常见的模型:经验性原子势模型和量子力学模型。经验性原子势模型在计算上高效但准确性有限,而量子力学模型虽然准确度高,但计算成本很高。近年来,机器学习(ML)模型开始崭露头角,用于解决准确性和效率之间的权衡问题。ML模型通过训练来建立原子配置和势能之间的关系,并能达到与量子力学方法相当的准确性,同时具有更低的计算成本。深度势(DP)模型是ML模型的一种,它不仅具有量子力学精度,而且具有高计算效率,并且是端到端的,支持在现代高性能计算机上高效运行。
DeePMD-kit 概述
DeePMD-kit 是一个使用深度学习模型来高效模拟分子动力学的工具包。下面是相关的参考内容:

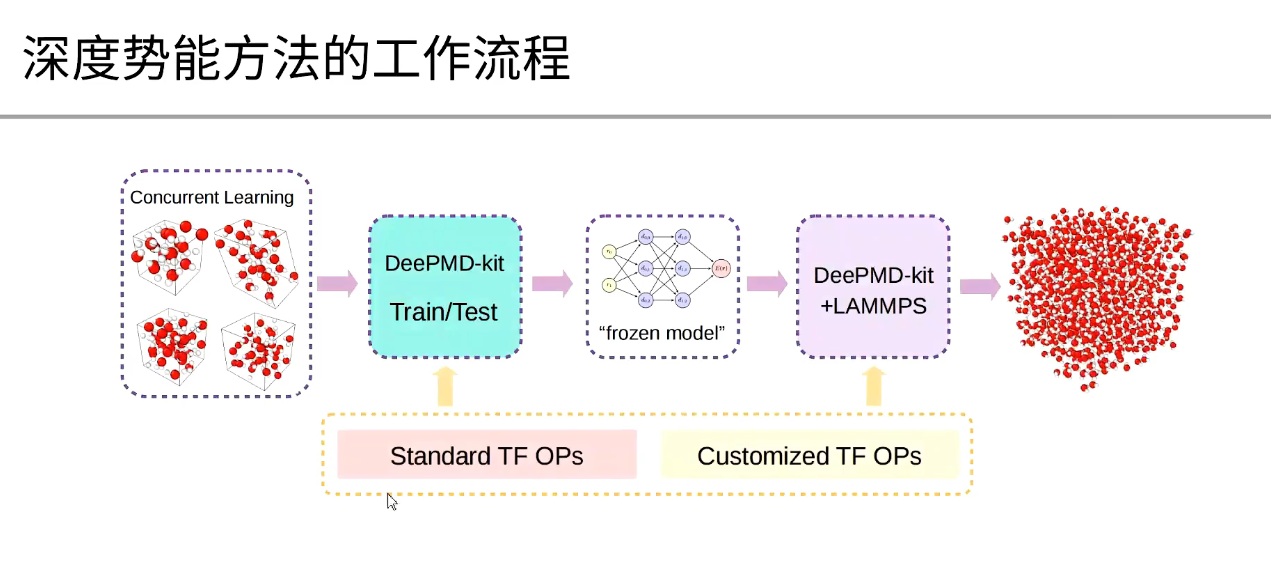
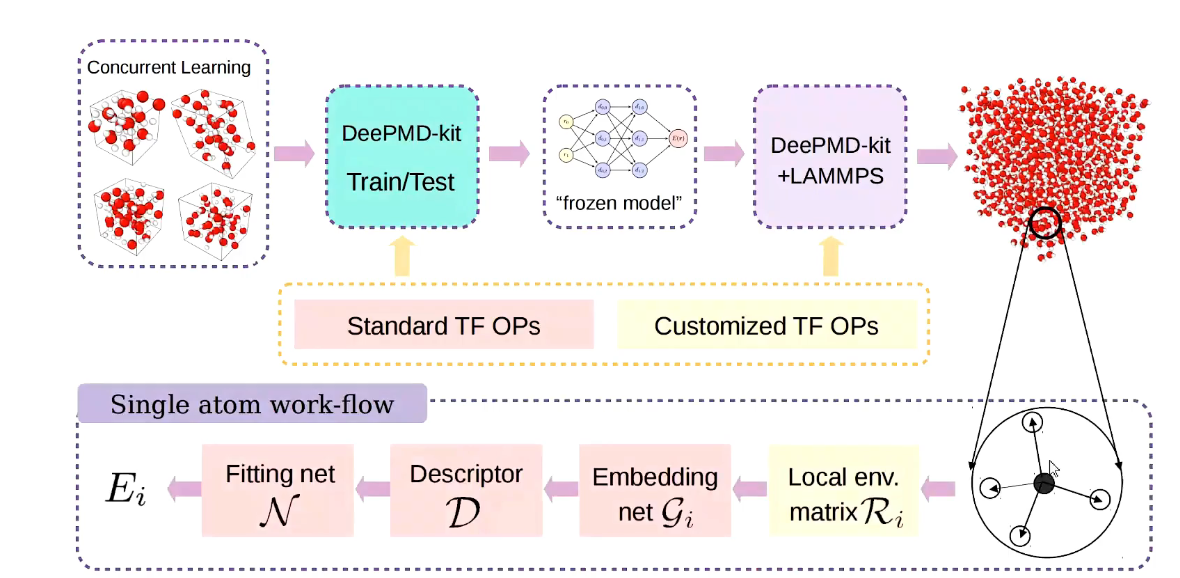
DeePMD-kit 的工作流程
准备训练数据:从量子力学模拟收集原子配置和相应的能量和力。
配置 DeePMD-kit:创建输入文件,指定训练数据、神经网络结构和训练参数。
描述符生成:DeePMD-kit 使用局部环境矩阵 $ \mathcal{R} $,它描述了特定原子及其邻居之间的距离和方向向量。
嵌入网络:将每个距离嵌入到 $ M_1 $ 维向量中,从而将环境矩阵 $ \mathcal{R} $ 嵌入到矩阵 $ \mathcal{G} $ 中。
拟合网络:通过矩阵乘法从 $ \mathcal{G} $ 中提取描述符向量,然后将描述符输入到拟合网络以获得预测能量。
原子类型嵌入:DeePMD-kit v2.0 允许在不同原子类型之间共享嵌入网络和拟合网络,从而降低训练复杂性。


DeePMD-kit 的原理
理论基础
在介绍DP方法之前,我们定义了一个包含N个原子的系统的坐标矩阵$\mathcal{R} \in \mathbb{R}^{N \times 3}$,
$$
\mathcal{R}=\left{\boldsymbol{r}1^T, \cdots, \boldsymbol{r}i^T, \cdots, \boldsymbol{r}N^T\right}^T, \boldsymbol{r}i=\left(x_i, y_i, z_i\right),(1)
$$
$\boldsymbol{r}i$包含原子$i$的3个笛卡尔坐标,$\boldsymbol{\mathcal { R }}$可以转换为局部环境矩阵$\left{\boldsymbol{\mathcal { R }}^i\right}{i=1}^N$
$$
\mathcal{R}^i=\left{\boldsymbol{r}{1 i}^T, \cdots, \boldsymbol{r}{j i}^T, \cdots, \boldsymbol{r}{N_i, i}^T\right}^T, \boldsymbol{r}{j i}=\left(x_{j i}, y_{j i}, z_{j i}\right),(2)
$$
其中$j$和$N_i$是原子$i$在截止半径$r_c$内的邻居的索引,$\boldsymbol{r}_{j i} \equiv \boldsymbol{r}_j-\boldsymbol{r}_i$被定义为相对坐标。
在DP方法中,系统的总能量$E$被构造为原子能量的总和。
$$
E=\sum_i E_i,(3)
$$
其中$E_i$是原子$i$的局部原子能量。$E_i$取决于原子$i$的局部环境:
$$
E=\sum_i E_i=\sum_i E\left(\mathcal{R}^i\right),(4)
$$
$\mathcal{R}^i$到$E_i$的映射分两步构造。如下图所示,

首先,$\mathcal{R}^i$被映射到一个特征矩阵,也称为描述符,$\mathcal{D}^i$,以保持系统的平移、旋转和排列对称性。$\mathcal{R}^i \in \mathbb{R}^{N_i \times 3}$首先被转换为广义坐标$\tilde{\mathcal{R}}^i \in \mathbb{R}^{N_i \times 4}$。
$$
\left{x_{j i}, y_{j i}, z_{j i}\right} \mapsto\left{s\left(r_{j i}\right), \hat{x}{j i}, \hat{y}{j i}, \hat{z}{j i}\right}
$$
其中$\hat{x}{j i}=\frac{s\left(r_{j j}\right) x x_{j i}}{r_{j i}}, \hat{y}{j i}=\frac{s\left(r{j j}\right) y \ddot{j}}{r_{j i}}$, 和 $\hat{z}{j i}=\frac{s\left(r{j j}\right) z j i}{r_{j i}}$。$s\left(r_{j i}\right)$是一个权重函数,用于减少离原子$i$较远的粒子的权重,定义为:
$$
s\left(r_{j i}\right)= \begin{cases}\frac{1}{r_{j i}}, & r_{j i}<r_{c s} \ \frac{1}{r_{j i}}\left{\left(\frac{r_{j i}-r_{c s}}{r_c-r_{c s}}\right)^3\left(-6\left(\frac{r_{j j}-r_{c s}}{r_c-r_{c s}}\right)^2+15 \frac{r_{j j}-r_{c s}}{r_c-r_{c s}}-10\right)+1\right}, & r_{c s}<r_{j i}<r_c,(6) \ 0, & r_{j i}>r_c\end{cases}
$$
这里$r_{j i}$是原子$i$和$j$之间的欧几里得距离,$r_{c s}$是平滑截止参数。通过引入$s\left(r_{j i}\right)$,$\tilde{\mathcal{R}}^i$中的分量从$r_{c s}$到$r_c$平滑地变为零。然后,$s\left(r_{j i}\right)$,即$\tilde{\mathcal{R}}^i$的第一列,通过嵌入神经网络映射到嵌入矩阵$\mathcal{G}^{i 2} \in \mathbb{R}^{N_i \times M_1}$。通过取$\mathcal{G}^{i 2} \in \mathbb{R}^{N_i \times M_2}$的前$M_2\left(<M_1\right)$列,我们得到另一个嵌入矩阵$\mathcal{G}^{i 2} \in \mathbb{R}^{N_i \times M_2}$。最后,我们定义原子$i$的特征矩阵$\mathcal{G}^{i 2} \in \mathbb{R}^{M_1 \times M_2}$:
$$
\mathcal{D}^i=\left(\mathcal{G}^{i 1}\right)^T \tilde{\mathcal{R}}^i\left(\tilde{\mathcal{R}}^i\right)^T \mathcal{G}^{i 2},(7)
$$
在特征矩阵中,通过$\tilde{\mathcal{R}}^i\left(\tilde{\mathcal{R}}^i\right)^T$的矩阵乘积保持平移和旋转对称性,并通过$\left(\mathcal{G}^i\right)^T \tilde{\mathcal{R}}^i$的矩阵乘积保持排列对称性。接下来,每个$\mathcal{D}^i$通过拟合网络映射到局部原子能量$E_i$。
嵌入网络$\mathcal{N}^e$和拟合网络$\mathcal{N}^f$都是包含几个隐藏层的前馈神经网络。从前一层的输入数据$d_l^{\text {in }}$到下一层的输出数据$d_k^{\text {out }}$的映射由线性和非线性变换组成。
$$
d_k^{o u t}=\varphi\left(\sum_{k l} w_{k l} d_l^{i n}+b_k\right),(8)
$$
在等式(8)中,$w_{k l}$是连接权重,$b_k$是偏置权重,$\varphi$是非线性激活函数。需要注意的是,只在输出节点应用线性变换。嵌入和拟合网络中包含的参数是通过最小化损失函数$L$获得的:
$$
L\left(p_\epsilon, p_f, p_{\xi}\right)=\frac{p_\epsilon}{N} \Delta \epsilon^2+\frac{p_f}{3 N} \sum_i\left|\Delta \boldsymbol{F}i\right|^2+\frac{p{\xi}}{9 N}|\Delta \xi|^2,(9)
$$
其中$\Delta \epsilon, \Delta \boldsymbol{F}i$, 和 $\Delta \xi$分别表示能量、力和应力的均方根误差。在训练过程中,前因子$p_\epsilon, p_f$, 和 $p{\xi}$由以下公式确定
$$
p(t)=p^{\operatorname{limit}}\left[1-\frac{r_l(t)}{r_l^0}\right]+p^{\operatorname{start}}\left[\frac{r_l(t)}{r_l^0}\right]
$$
其中$r_l(t)$和$r_l^0$分别是训练步骤$t$和训练步骤0的学习率。$r_l(t)$定义为
$$
r_l(t)=r_l^0 \times d_r^{t / d_s}
$$
其中$d_r$和$d_s$分别是衰减率和衰减步骤。衰减率$d_r$需要小于1。有关DeepPot-SE (DP)方法的详细信息,请参阅原始论文。
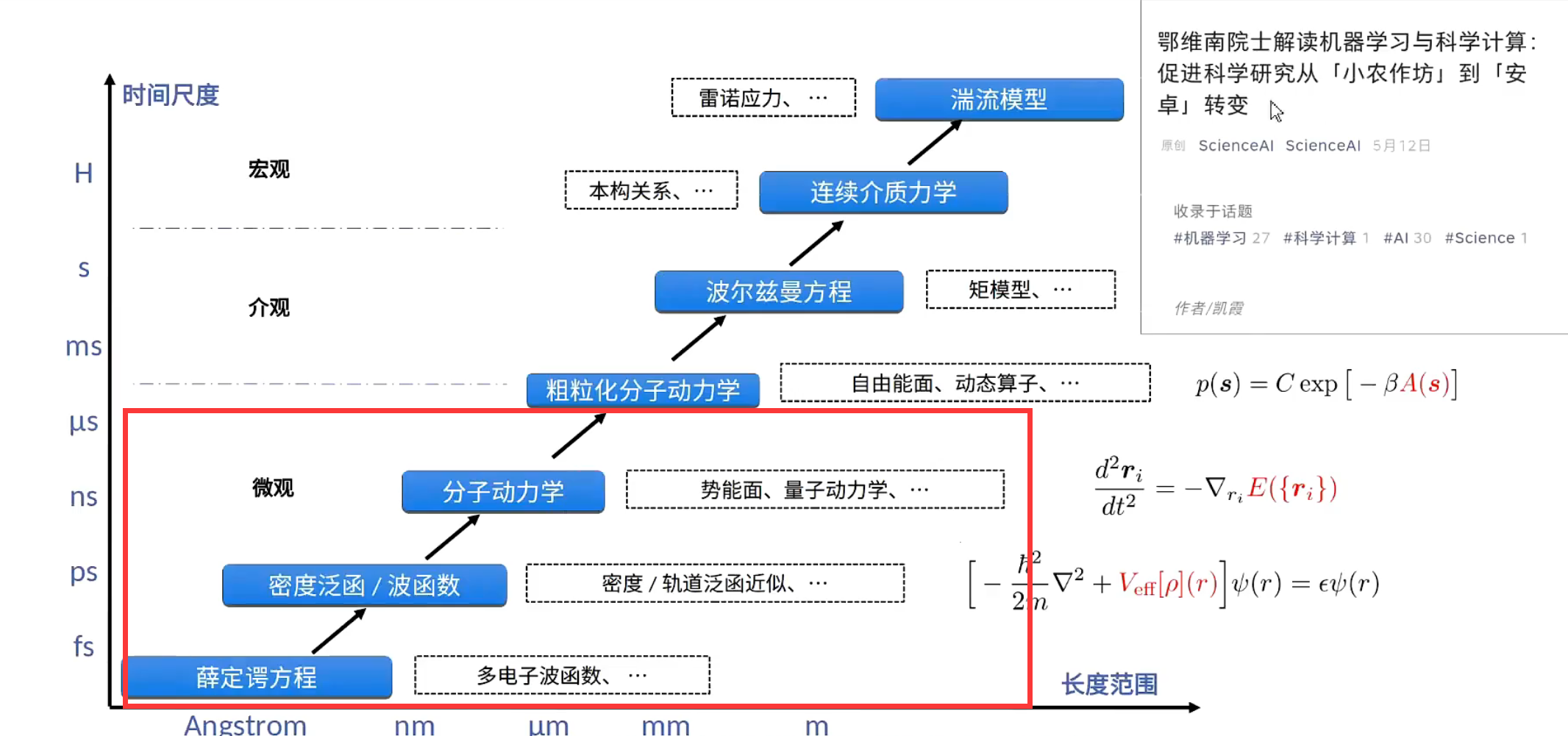
分子动力学
分子动力学模拟是一种从微观出发的模拟手段,在科学发现,工程设计等领域具有重要作用。
$$
\begin{aligned}
& m_i \frac{d^2 \boldsymbol{r}_i}{d t^2}=-\nabla_i E \
& E=E\left(\boldsymbol{r}_1, \boldsymbol{r}_2, \ldots, \boldsymbol{r}_N\right)
\end{aligned}
$$
- 计算能量的常见的方式
| 方法 | 例子 | 优缺点 |
|---|---|---|
| 第一性原理计算密度泛函理论(DFT) | 密度泛函理论(DFT) | 精度高,计算复杂度高 |
| 计算经验力场 | LJ,EAM,MEAM | 计算复杂度低,精度不可靠 |
DeePKS(电子结构)

满足要求比较好的是单电子的密度矩阵, 然后把波函数投影到一组比较好的完备基上。

 构建过程
构建过程

- 给定原子坐标, 写出电子结构, 利用DFT计算得到能量, 构建坐标能量对,典型的
监督学习,回归问题。 - 利用DNN来构建
体系坐标和能量的关系。
常见的问题:
- 物理约束(旋转性,对称性, 平移, 交换…)

- 小原子数量训练得到的在大体系上是否存在问题?
深度势能的构建关系
$$
E=\sum_i \mathcal{N}{\alpha_i}\left(\mathcal{D}{\alpha_i}\left(r_i,\left{r_j\right}_{j \in n(i)}\right)\right)
$$

Function $f\left(x_1, x_2, \ldots x_N\right)$ is permutationally invariant if and only if there exist $\rho$ and $\phi$ such that $f\left(\left{x_i\right}\right)=\rho\left(\sum_i \phi\left(x_i\right)\right)$
$$
\mathcal{R}i=\left(\begin{array}{cccc}
1 / r{i 1} & x_{i 1} / r_{i 1}^2 & y_{i 1} / r_{i 1}^2 & z_{i 1} / r_{i 1}^2 \
1 / r_{i 2} & x_{i 2} / r_{i 2}^2 & y_{i 2} / r_{i 2}^2 & z_{i 2} / r_{i 2}^2 \
1 / r_{i 3} & x_{i 3} / r_{i 3}^2 & y_{i 3} / r_{i 3}^2 & z_{i 3} / r_{i 3}^2 \
\vdots & \vdots & \vdots & \vdots
\end{array}\right) \
\mathcal{G}_i=\left(\begin{array}{cccc}
G_1\left(r_{i 1}\right) G_2\left(r_{i 1}\right) & G_3\left(r_{i 1}\right) & \cdots \
G_1\left(r_{i 2}\right) & G_2\left(r_{i 2}\right) & G_3\left(r_{i 2}\right) & \cdots \
G_1\left(r_{i 3}\right) & G_2\left(r_{i 3}\right) & G_3\left(r_{i 3}\right) & \cdots \
\vdots & \vdots & \vdots & \ddots
\end{array}\right)
$$
R: 环境矩阵, 对于每一个原子来说的, 元素是原子之间的相对距离,所以满足平移相对性,
G: embedding matrix。

周期不变:
$$
\mathcal{D}_i=\left(\mathcal{G}_i^{<}\right)^T \mathcal{R}_i\left(\mathcal{R}_i\right)^T \mathcal{G}_i
$$
旋转不变:
$$
\tilde{\mathcal{D}}_i=\left(\mathcal{G}_i\right)^T\left(\mathcal{R}_i U\right)\left(\mathcal{R}_i U\right)^T \mathcal{G}_i=\left(\mathcal{G}_i\right)^T \mathcal{R}_i U U^T \mathcal{R}_i \mathcal{G}_i=\mathcal{D}_i
$$
神经网络的构建:

数据集构建
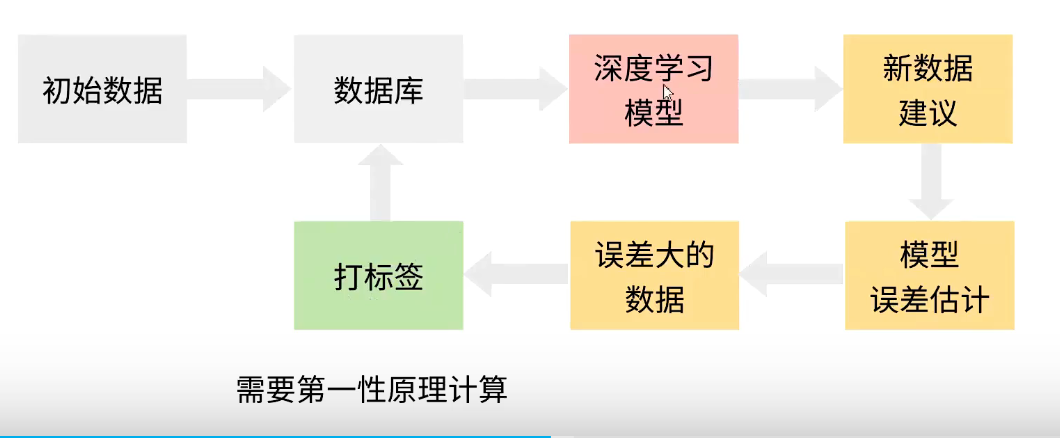
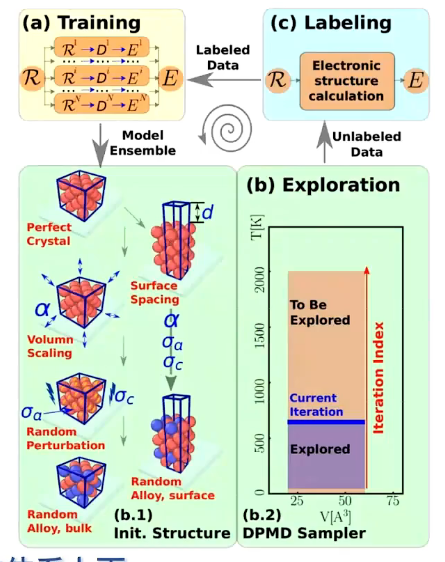
需要保证,大体系结构中的局部体系的结果都在数据集里面有实现。
DeePMD-kit 的代码实现
代码修改: DeePMD-kit 的代码实现涉及到几个主要部分,包括trainer,model,embedding net 和 fitting net。trainer 部分解析输入 JSON 文件中的参数。model 部分构建操作图,包括type embed net,embedding net 和 fitting net。embedding net 接收环境矩阵 $ \mathcal{R} $ 作为输入,并输出矩阵 $ \mathcal{G} $。fitting net 接收描述符向量作为输入,并输出能量预测。
模型训练的代码:
class EnerModel(Model):
# 定义一个名为EnerModel的类,继承自Model基类
# 用于表示能量模型
# 类变量,表示模型类型
model_type = "ener"
def __init__(
self,
descrpt,
fitting,
typeebd=None,
type_map: Optional[List[str]] = None,
data_stat_nbatch: int = 10,
data_stat_protect: float = 1e-2,
use_srtab: Optional[str] = None,
smin_alpha: Optional[float] = None,
sw_rmin: Optional[float] = None,
sw_rmax: Optional[float] = None,
spin: Optional[Spin] = None,
) -> None:
# 构造函数,初始化EnerModel类的实例
# 将描述符赋值给实例变量descrpt
self.descrpt = descrpt
# 从描述符中获取截断半径,并赋值给实例变量rcut
self.rcut = self.descrpt.get_rcut()
# 从描述符中获取原子类型的数量,并赋值给实例变量ntypes
self.ntypes = self.descrpt.get_ntypes()
# 将拟合网络赋值给实例变量fitting
self.fitting = fitting
# 从拟合网络中获取参数数量,并赋值给实例变量numb_fparam
self.numb_fparam = self.fitting.get_numb_fparam()
# 将类型嵌入赋值给实例变量typeebd
self.typeebd = typeebd
# 将自旋赋值给实例变量spin
self.spin = spin
# 如果type_map为None,则将空列表赋值给实例变量type_map,否则将type_map赋值给实例变量type_map
if type_map is None:
self.type_map = []
else:
self.type_map = type_map
# 将data_stat_nbatch赋值给实例变量data_stat_nbatch
self.data_stat_nbatch = data_stat_nbatch
# 将data_stat_protect赋值给实例变量data_stat_protect
self.data_stat_protect = data_stat_protect
# 将use_srtab赋值给实例变量srtab_name
self.srtab_name = use_srtab
# 如果srtab_name不为None,则初始化PairTab并赋值给实例变量srtab,并将smin_alpha, sw_rmin, sw_rmax赋值给相应的实例变量
if self.srtab_name is not None:
self.srtab = PairTab(self.srtab_name)
self.smin_alpha = smin_alpha
self.sw_rmin = sw_rmin
self.sw_rmax = sw_rmax
# 否则,将None赋值给实例变量srtab
else:
self.srtab = None
定义神经网络的部分:
- embedding_net
其中描述符 部分主要由这个embedding_net构成
def embedding_net(
xx,
network_size,
precision,
activation_fn=tf.nn.tanh,
resnet_dt=False,
name_suffix="",
stddev=1.0,
bavg=0.0,
seed=None,
trainable=True,
uniform_seed=False,
initial_variables=None,
mixed_prec=None,
):
r"""The embedding network.
The embedding network function :math:`\mathcal{N}` is constructed by is the
composition of multiple layers :math:`\mathcal{L}^{(i)}`:
.. math::
\mathcal{N} = \mathcal{L}^{(n)} \circ \mathcal{L}^{(n-1)}
\circ \cdots \circ \mathcal{L}^{(1)}
A layer :math:`\mathcal{L}` is given by one of the following forms,
depending on the number of nodes: [1]_
.. math::
\mathbf{y}=\mathcal{L}(\mathbf{x};\mathbf{w},\mathbf{b})=
\begin{cases}
\boldsymbol{\phi}(\mathbf{x}^T\mathbf{w}+\mathbf{b}) + \mathbf{x}, & N_2=N_1 \\
\boldsymbol{\phi}(\mathbf{x}^T\mathbf{w}+\mathbf{b}) + (\mathbf{x}, \mathbf{x}), & N_2 = 2N_1\\
\boldsymbol{\phi}(\mathbf{x}^T\mathbf{w}+\mathbf{b}), & \text{otherwise} \\
\end{cases}
where :math:`\mathbf{x} \in \mathbb{R}^{N_1}` is the input vector and :math:`\mathbf{y} \in \mathbb{R}^{N_2}`
is the output vector. :math:`\mathbf{w} \in \mathbb{R}^{N_1 \times N_2}` and
:math:`\mathbf{b} \in \mathbb{R}^{N_2}` are weights and biases, respectively,
both of which are trainable if `trainable` is `True`. :math:`\boldsymbol{\phi}`
is the activation function.
Parameters
----------
xx : Tensor
Input tensor :math:`\mathbf{x}` of shape [-1,1]
network_size : list of int
Size of the embedding network. For example [16,32,64]
precision:
Precision of network weights. For example, tf.float64
activation_fn:
Activation function :math:`\boldsymbol{\phi}`
resnet_dt : boolean
Using time-step in the ResNet construction
name_suffix : str
The name suffix append to each variable.
stddev : float
Standard deviation of initializing network parameters
bavg : float
Mean of network intial bias
seed : int
Random seed for initializing network parameters
trainable : boolean
If the network is trainable
uniform_seed : boolean
Only for the purpose of backward compatibility, retrieves the old behavior of using the random seed
initial_variables : dict
The input dict which stores the embedding net variables
mixed_prec
The input dict which stores the mixed precision setting for the embedding net
References
----------
.. [1] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Identitymappings
in deep residual networks. InComputer Vision – ECCV 2016,pages 630–645. Springer
International Publishing, 2016.
"""
input_shape = xx.get_shape().as_list()
outputs_size = [input_shape[1]] + network_size
for ii in range(1, len(outputs_size)):
w_initializer = tf.random_normal_initializer(
stddev=stddev / np.sqrt(outputs_size[ii] + outputs_size[ii - 1]),
seed=seed if (seed is None or uniform_seed) else seed + ii * 3 + 0,
)
b_initializer = tf.random_normal_initializer(
stddev=stddev,
mean=bavg,
seed=seed if (seed is None or uniform_seed) else seed + 3 * ii + 1,
)
if initial_variables is not None:
scope = tf.get_variable_scope().name
w_initializer = tf.constant_initializer(
initial_variables[scope + "/matrix_" + str(ii) + name_suffix]
)
b_initializer = tf.constant_initializer(
initial_variables[scope + "/bias_" + str(ii) + name_suffix]
)
w = tf.get_variable(
"matrix_" + str(ii) + name_suffix,
[outputs_size[ii - 1], outputs_size[ii]],
precision,
w_initializer,
trainable=trainable,
)
variable_summaries(w, "matrix_" + str(ii) + name_suffix)
b = tf.get_variable(
"bias_" + str(ii) + name_suffix,
[outputs_size[ii]],
precision,
b_initializer,
trainable=trainable,
)
variable_summaries(b, "bias_" + str(ii) + name_suffix)
if mixed_prec is not None:
xx = tf.cast(xx, get_precision(mixed_prec["compute_prec"]))
w = tf.cast(w, get_precision(mixed_prec["compute_prec"]))
b = tf.cast(b, get_precision(mixed_prec["compute_prec"]))
if activation_fn is not None:
hidden = tf.reshape(
activation_fn(tf.nn.bias_add(tf.matmul(xx, w), b)),
[-1, outputs_size[ii]],
)
else:
hidden = tf.reshape(
tf.nn.bias_add(tf.matmul(xx, w), b), [-1, outputs_size[ii]]
)
if resnet_dt:
idt_initializer = tf.random_normal_initializer(
stddev=0.001,
mean=1.0,
seed=seed if (seed is None or uniform_seed) else seed + 3 * ii + 2,
)
if initial_variables is not None:
scope = tf.get_variable_scope().name
idt_initializer = tf.constant_initializer(
initial_variables[scope + "/idt_" + str(ii) + name_suffix]
)
idt = tf.get_variable(
"idt_" + str(ii) + name_suffix,
[1, outputs_size[ii]],
precision,
idt_initializer,
trainable=trainable,
)
variable_summaries(idt, "idt_" + str(ii) + name_suffix)
if mixed_prec is not None:
idt = tf.cast(idt, get_precision(mixed_prec["compute_prec"]))
if outputs_size[ii] == outputs_size[ii - 1]:
if resnet_dt:
xx += hidden * idt
else:
xx += hidden
elif outputs_size[ii] == outputs_size[ii - 1] * 2:
if resnet_dt:
xx = tf.concat([xx, xx], 1) + hidden * idt
else:
xx = tf.concat([xx, xx], 1) + hidden
else:
xx = hidden
if mixed_prec is not None:
xx = tf.cast(xx, get_precision(mixed_prec["output_prec"]))
return xx
这个embedding_net函数定义了一个嵌入神经网络,通常用于将输入数据转换为更高维的表示,以便于进一步的处理。这个网络是由多个全连接层组成的,并且可以选择使用残差连接(ResNet风格)。
神经网络的结构如下:
- 输入是一个张量
xx,形状为[-1, 1]。 network_size参数是一个列表,表示每个隐藏层的节点数。例如,network_size = [16, 32, 64]表示有三个隐藏层,分别有16、32和64个节点。- 对于每个隐藏层,它执行以下操作:
- 线性变换:
y = x * W + b,其中W是权重矩阵,b是偏置向量。 - 激活函数:可选的非线性激活函数,如tanh。
- 可选的残差连接:如果启用
resnet_dt,并且输入和输出的维度相同,则将输入加回到输出。
- 线性变换:
graph TD
classDef largeNode font-size:20px;
class A,B,C,D,E,F largeNode;
A[Input]
B[全连接层<br>激活函数]
C[全连接层<br>激活函数]
D[...]
E[全连接层<br>激活函数]
F[Output]
A --> B
B --> C
C --> D
D --> E
E --> F
- fitting_network
fitting_network是这个网络主要由全连接构成,下面的给出是每一层全连接的定义。
def one_layer(
inputs,
outputs_size,
activation_fn=tf.nn.tanh,
precision=GLOBAL_TF_FLOAT_PRECISION,
stddev=1.0,
bavg=0.0,
name="linear",
reuse=None,
seed=None,
use_timestep=False,
trainable=True,
useBN=False,
uniform_seed=False,
initial_variables=None,
mixed_prec=None,
final_layer=False,
):
r"""Build one layer with continuous or quantized value.
Its weight and bias can be initialed with random or constant value.
"""
# USE FOR NEW FITTINGNET
with tf.variable_scope(name, reuse=reuse):
shape = inputs.get_shape().as_list()
w, b = one_layer_wb(
shape,
outputs_size,
bavg,
stddev,
precision,
trainable,
initial_variables,
seed,
uniform_seed,
name,
)
if nvnmd_cfg.quantize_fitting_net:
NBIT_DATA_FL = nvnmd_cfg.nbit["NBIT_FIT_DATA_FL"]
NBIT_SHORT_FL = nvnmd_cfg.nbit["NBIT_FIT_SHORT_FL"]
# w
with tf.variable_scope("w", reuse=reuse):
w = op_module.quantize_nvnmd(w, 1, NBIT_DATA_FL, NBIT_DATA_FL, -1)
w = tf.ensure_shape(w, [shape[1], outputs_size])
# b
with tf.variable_scope("b", reuse=reuse):
b = op_module.quantize_nvnmd(b, 1, NBIT_DATA_FL, NBIT_DATA_FL, -1)
b = tf.ensure_shape(b, [outputs_size])
# x
with tf.variable_scope("x", reuse=reuse):
x = op_module.quantize_nvnmd(inputs, 1, NBIT_DATA_FL, NBIT_DATA_FL, -1)
inputs = tf.ensure_shape(x, [None, shape[1]])
# wx
# normlize weight mode: 0 all | 1 column
norm_mode = 0 if final_layer else 1
wx = op_module.matmul_fitnet_nvnmd(
inputs, w, NBIT_DATA_FL, NBIT_SHORT_FL, norm_mode
)
with tf.variable_scope("wx", reuse=reuse):
wx = op_module.quantize_nvnmd(wx, 1, NBIT_DATA_FL, NBIT_DATA_FL - 2, -1)
wx = tf.ensure_shape(wx, [None, outputs_size])
# wxb
wxb = wx + b
with tf.variable_scope("wxb", reuse=reuse):
wxb = op_module.quantize_nvnmd(wxb, 1, NBIT_DATA_FL, NBIT_DATA_FL, -1)
wxb = tf.ensure_shape(wxb, [None, outputs_size])
# actfun
if activation_fn is not None:
# set activation function as tanh4
y = op_module.tanh4_flt_nvnmd(wxb)
else:
y = wxb
with tf.variable_scope("actfun", reuse=reuse):
y = op_module.quantize_nvnmd(y, 1, NBIT_DATA_FL, NBIT_DATA_FL, -1)
y = tf.ensure_shape(y, [None, outputs_size])
else:
hidden = tf.matmul(inputs, w) + b
# set activation function as tanh4
y = tanh4(hidden) if (activation_fn is not None) else hidden
# 'reshape' is necessary
# the next layer needs shape of input tensor to build weight
y = tf.reshape(y, [-1, outputs_size])
return y
这个函数的主要特点是它支持量化值,这是一种在神经网络中使用低精度表示的技术,通常用于减少内存使用和计算开销。此外,它使用自定义的激活函数op_module.tanh4_flt_nvnmd,这可能是一个对标准tanh函数的变种或近似。
graph TD
classDef largeNode font-size:16px;
class A,B,C,D,E,F,G,H,I,J,K,L,M,N,O largeNode;
A[输入: inputs, weights, bias]
B[创建变量作用域]
C[获取输入形状并初始化权重和偏差]
D[量化启用?]
E[对权重进行量化]
F[对偏差进行量化]
G[对输入进行量化]
H[执行量化的矩阵乘法]
I[添加偏差]
J[应用激活函数]
K[执行常规全连接层操作]
L[应用激活函数]
M[重新整形输出]
N[返回输出]
A --> B
B --> C
C --> D
D -- Yes --> E
E --> F
F --> G
G --> H
H --> I
I --> J
J --> M
D -- No --> K
K --> L
L --> M
M --> N
实际上,定义这个网络的参数为(修改网络可能得动源代码):
{
"_comment": " model parameters",
"model": {
"descriptor": {
"type": "se_a",
"sel": [
46,
92
],
"rcut_smth": 5.80,
"rcut": 6.00,
"neuron": [
25,
50,
100
],
"resnet_dt": false,
"axis_neuron": 16,
"seed": 1
},
"fitting_net": {
"neuron": [
240,
240,
240
],
"resnet_dt": true,
"seed": 1
}
},
"_comment": " traing controls",
"systems": [
"system"
],
"set_prefix": "set",
"stop_batch": 1000000,
"batch_size": 1,
"start_lr": 0.005,
"decay_steps": 5000,
"decay_rate": 0.95,
"start_pref_e": 0.02,
"limit_pref_e": 1,
"start_pref_f": 1000,
"limit_pref_f": 1,
"start_pref_v": 0,
"limit_pref_v": 0,
"seed": 1,
"_comment": " display and restart",
"_comment": " frequencies counted in batch",
"disp_file": "lcurve.out",
"disp_freq": 100,
"numb_test": 1,
"save_freq": 1000,
"save_ckpt": "model.ckpt",
"load_ckpt": "model.ckpt",
"disp_training": true,
"time_training": true,
"profiling": false,
"profiling_file": "timeline.json",
"_comment": "that's all"
}
实际上,使用这个过程包括:
定义embedding和fitting神经网络
jdata["model"]["descriptor"].pop("type", None)
descrpt = DescrptSeAEbd(
**jdata["model"]["descriptor"],
)
jdata["model"]["fitting_net"]["descrpt"] = descrpt
fitting = EnerFitting(
**jdata["model"]["fitting_net"],
)
model = EnerModel(descrpt, fitting)
定义输入张量
input_data = {
"coord": [test_data["coord"]],
"box": [test_data["box"]],
"type": [test_data["type"]],
"natoms_vec": [test_data["natoms_vec"]],
"default_mesh": [test_data["default_mesh"]],
}
推理
这里可以计算得到能量,受力,维里张量,输入原子。
model._compute_input_stat(input_data)
model.descrpt.bias_atom_e = data.compute_energy_shift()
t_prop_c = tf.placeholder(tf.float32, [5], name="t_prop_c")
t_energy = tf.placeholder(GLOBAL_ENER_FLOAT_PRECISION, [None], name="t_energy")
t_force = tf.placeholder(GLOBAL_TF_FLOAT_PRECISION, [None], name="t_force")
t_virial = tf.placeholder(GLOBAL_TF_FLOAT_PRECISION, [None], name="t_virial")
t_atom_ener = tf.placeholder(
GLOBAL_TF_FLOAT_PRECISION, [None], name="t_atom_ener"
)
t_coord = tf.placeholder(GLOBAL_TF_FLOAT_PRECISION, [None], name="i_coord")
t_type = tf.placeholder(tf.int32, [None], name="i_type")
t_natoms = tf.placeholder(tf.int32, [model.ntypes + 2], name="i_natoms")
t_box = tf.placeholder(GLOBAL_TF_FLOAT_PRECISION, [None, 9], name="i_box")
t_mesh = tf.placeholder(tf.int32, [None], name="i_mesh")
is_training = tf.placeholder(tf.bool)
t_fparam = None
model_pred = model.build(
t_coord,
t_type,
t_natoms,
t_box,
t_mesh,
t_fparam,
suffix="se_a_ebd",
reuse=False,
)
energy = model_pred["energy"]
force = model_pred["force"]
virial = model_pred["virial"]
atom_ener = model_pred["atom_ener"]
训练和验证
使用大量的训练数据(原子配置和相应的能量和力)来训练 DeePMD-kit 模型的神经网络。通过最小化模型预测和实际能量和力之间的差异来调整网络的权重。训练完成后,模型需要使用新数据进行验证,以评估其性能。这涉及将模型在训练期间未见过的原子配置输入,并将模型的预测与实际能量和力进行比较。
模拟
一旦模型经过训练和验证,它就可以用于分子动力学模拟。
应用案例
展示 DeePMD-kit 在实际问题中的应用。
Deep Potential Molecular Dynamics: a scalable model with the accuracy of quantum mechanics
DeepMD提出的原始论文, 包含其中的原理部分。
(2017年)
- 作者:Linfeng Zhang, Jiequn Han, Han Wang, R. Car, E. Weinan
- 被引用次数:673次
- 摘要:该论文介绍了一种基于深度神经网络的分子模拟方案,称为深度势能分子动力学(DPMD)方法。该神经网络模型保留了问题中的所有自然对称性,并且是基于第一性原理的,除了网络模型之外没有任何特设组件。该方案在各种系统中提供了一种高效且准确的协议,包括体材料和分子。在所有这些情况下,DPMD给出的结果与原始数据基本上是无法区分的,而且成本与系统大小成线性关系。
- PDF链接
-
DeepMD-KIt提出的原始论文, 主要是其中的代码实现以及benchmark。
- 作者:Han Wang, Linfeng Zhang, Jiequn Han, E. Weinan
- 被引用次数:485次
- 摘要:该论文描述了DeePMD-kit,这是一个用Python/C++编写的包,旨在最小化构建基于深度学习的势能和力场表示以及执行分子动力学所需的工作。DeePMD-kit的潜在应用范围从有限分子到扩展系统,从金属系统到化学键合系统。DeePMD-kit与TensorFlow(最受欢迎的深度学习框架之一)接口,使训练过程高度自动化和高效。
- PDF链接
-
- 作者:Weile Jia, Han Wang, Mohan Chen, Denghui Lu, Jiduan Liu, Lin Lin, R. Car, E. Weinan, Linfeng Zhang
- 被引用次数:124次
- 摘要:该论文报告了一种基于机器学习的模拟协议(Deep Potential Molecular Dynamics),在保持从头算精度的同时,可以每天模拟超过1纳秒长的超过1亿原子的轨迹。该代码可以高效地扩展到整个Summit超级计算机,在双精度下达到91 PFLOPS(峰值的45.5%),在混合单精度/半精度下达到162/275 PFLOPS。这项工作的重大成就是,它为以从头算精度模拟前所未有的大小和时间尺度打开了大门。
- PDF链接
作者通过使用一种称为“自动混合精度”(Automatic Mixed Precision, AMP)的技术来实现GPU加速。AMP是一种使用混合精度算法的技术,它结合了单精度(FP32)和半精度(FP16)浮点数来加速模型的训练和推理。
- 混合精度训练:AMP 使用混合精度训练,这意味着它在训练过程中同时使用16位和32位浮点数。这种方法可以减少内存使用量和计算时间。
- 保持精度:虽然使用较低的精度可以加速训练,但是可能会导致精度下降。AMP 使用一种称为“损失缩放”的技术来防止在低精度计算中丢失过多的信息。
- 动态损失缩放:AMP 使用动态损失缩放。这意味着它会自动调整损失缩放的因子,以防止数值下溢和过溢。
- 优化器状态保持为FP32:AMP 会将模型的权重存储为16位浮点数以节省内存,但是优化器的状态(例如,Adam优化器的移动平均值)仍然保持为32位浮点数,以保持训练的数值稳定性。
文章中还提到了使用Tensor Cores,这是一种专门的硬件加速器,用于加速混合精度矩阵乘法和卷积计算。通过使用Tensor Cores,AMP可以进一步提高性能和吞吐量。
- 高效矩阵运算:Tensor Cores 是专门设计用于执行混合精度矩阵乘法和加法的硬件单元。这对于深度学习中的许多操作(如卷积和全连接层)非常重要。
- 混合精度:Tensor Cores 可以在16位浮点数上执行乘法,并将结果累加到32位浮点数。这允许它们在保持精度的同时执行更快的计算。
- 加速深度学习训练和推理:通过使用Tensor Cores,可以显著加速深度学习模型的训练和推理过程。
- 硬件支持:Tensor Cores 是NVIDIA的Volta和更新的GPU架构的一部分。这意味着只有支持这些架构的硬件才能利用Tensor Cores。
- 与AMP结合:在论文中,Tensor Cores 与自动混合精度(AMP)一起使用,以进一步优化和加速深度学习训练
86 PFLOPS Deep Potential Molecular Dynamics simulation of 100 million atoms with ab initio accuracy (2020年)
- 作者:Denghui Lu, Han Wang, Mohan Chen, Jiduan Liu, Lin Lin, R. Car, E. Weinan, Weile Jia, Linfeng Zhang
- 被引用次数:88次
- 摘要:该论文介绍了DeePMD-kit的GPU版本,通过使用从头算数据训练深度神经网络模型,可以进行具有从头算精度的极大规模分子动力学(MD)模拟。测试表明,与CPU版本相比,GPU版本在相同的功耗下速度快7倍。该代码可以扩展到整个Summit超级计算机。对于一个包含113,246,208个原子的铜系统,该代码每天可以执行一纳秒的MD模拟,达到86 PFLOPS的峰值性能(峰值的43%)。
- PDF链接
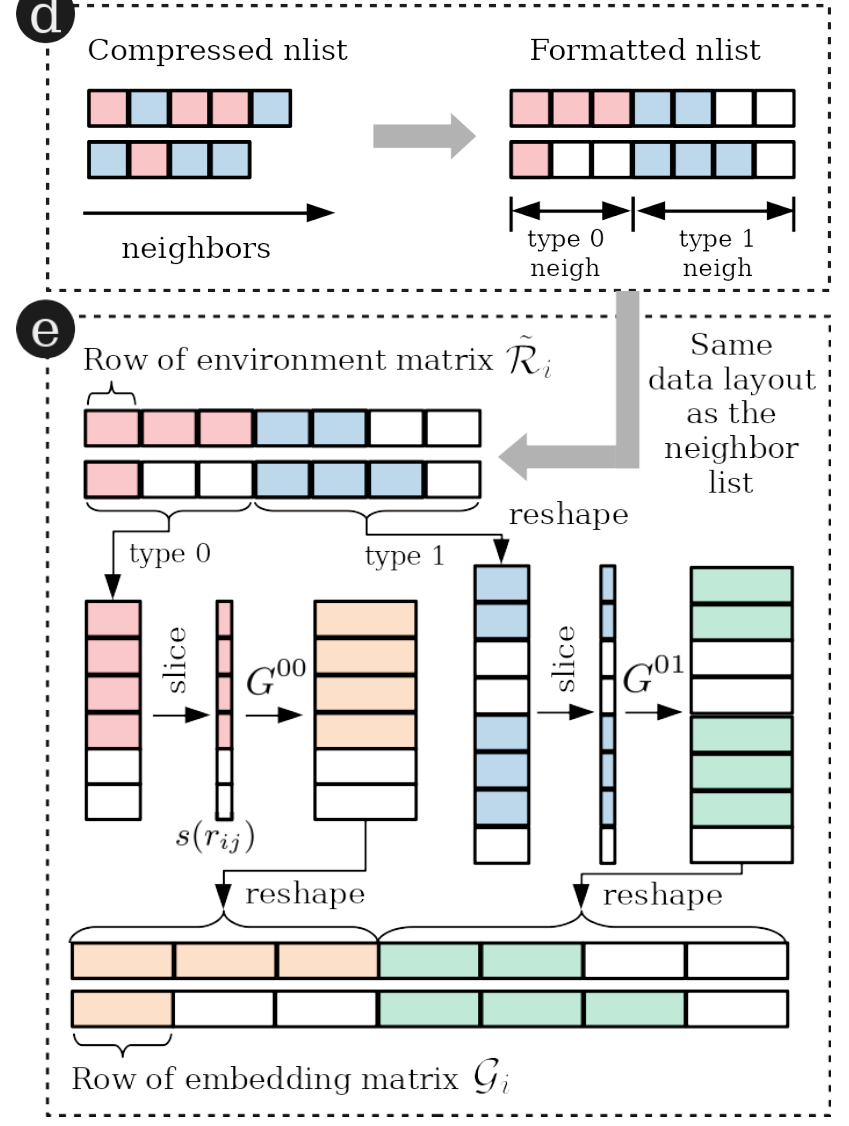
- 通过自制TensorFlow算子来实现加速。
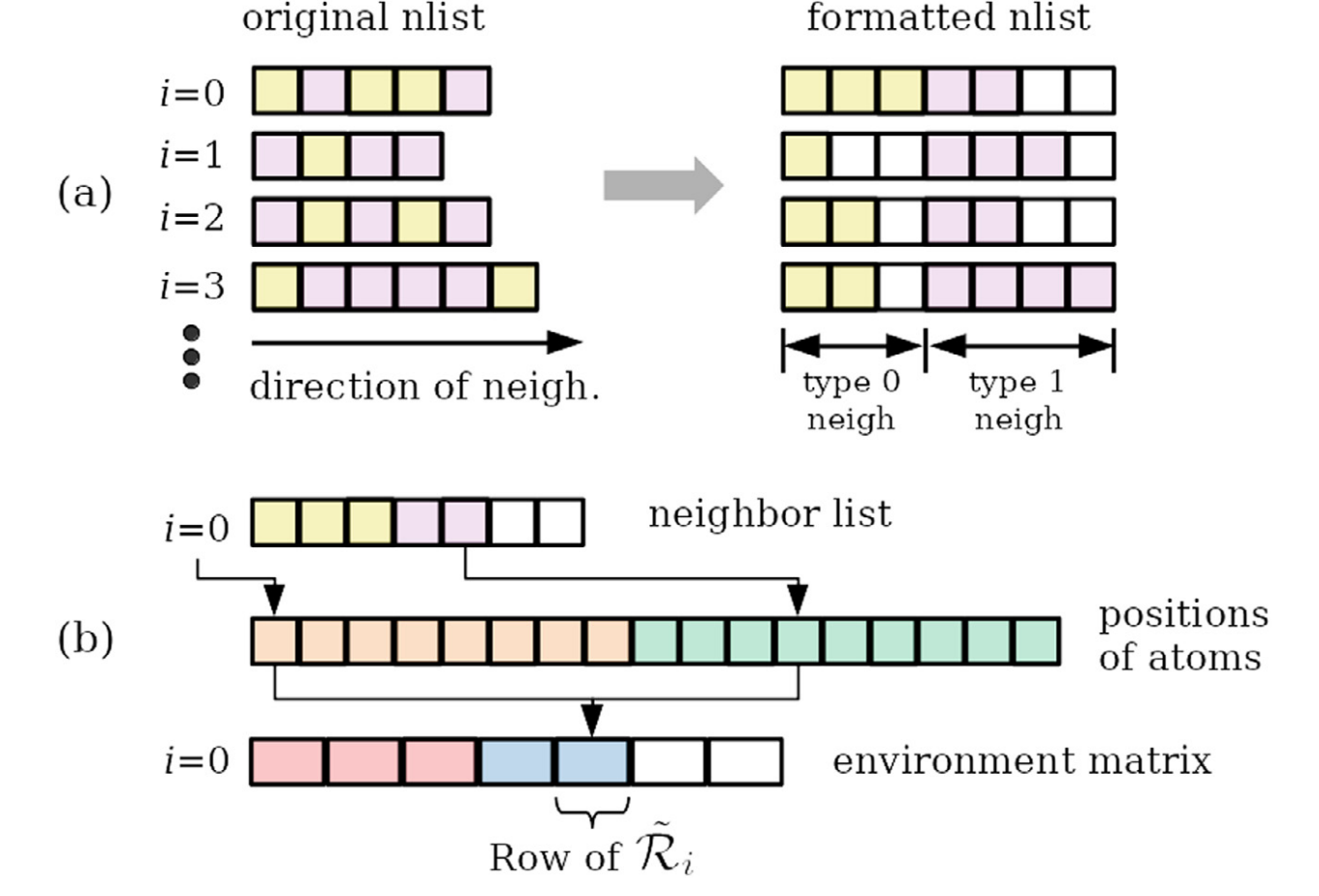
- 形成和格式化邻居列表:这一步骤中,将相邻的元素(或原子)按照它们的类型进行分类和排序。在图示中,黄色方块表示一种类型的邻居,紫色方块表示另一种类型的邻居。邻居首先按类型排序,然后按距离和原子索引排序。列表中的空白方块用于填充。
- 计算环境矩阵:在这一步,使用上一步得到的格式化邻居列表来计算环境矩阵。这个矩阵可能包含了与邻居的相互作用或其他物理属性有关的信息。
A Deep Potential model for liquid-vapor equilibrium and cavitation rates of water (2023年1月27日)
作者:I. Sanchez-Burgos, M. Muniz, J. R. Espinosa, A. Panagiotopoulos
摘要:本文利用Deep Potential方法研究水的液-气相平衡和空化率。通过机器学习模型,研究了液-气共存区的相图。机器学习模型是基于SCAN密度泛函的从头算能量和力来训练的。文章计算了一系列温度下的表面张力、饱和压力和汽化焓,并评估了Deep Potential模型的性能。此外,通过使用播种技术,评估了负压下的自由能障碍和成核率。这项工作是Deep Potential模型在研究液-气共存和水空化方面的首次应用。
具体实现内容:
- DPMD模型的数据在温度上被偏移了40 K,以更准确地模拟给定温度下的行为。这个偏移是通过计算模型预测的共存蒸汽密度与实验值之间的均方误差来调整的。
- 在液-气平衡区域,DPMD模型的密度略高于实验结果(在低温下,<500 K),但在较高温度下与实验结果相符。
- DPMD模型的临界温度为632.6 K,比实验值低14.5 K。
- DPMD模型预测的液-气表面张力值低于TIP4P/2005模型和实验测量值。
- DPMD模型的饱和蒸汽压与实验测量值非常接近,而TIP4P/2005模型则低估了这个值。

这几个图表共同展示了深度势能分子动力学(DPMD)模型在模拟水的液-气平衡性质方面的性能。通过将模型的预测结果与另一个称为TIP4P/2005的模型以及实验数据进行比较,图表揭示了DPMD模型在不同方面的准确性。
- 图2(a) 和其插图主要关注模型对水在不同温度下的密度的预测。这是通过在温度-密度平面上的相图来展示的,其中插图提供了模拟的可视化。
- 图2(b) 着重于展示模型对液-气界面自由能(表面张力)随温度变化的预测。
- 图2(c) 及其插图则展示了模型对饱和蒸汽压和汽化焓随温度变化的预测。
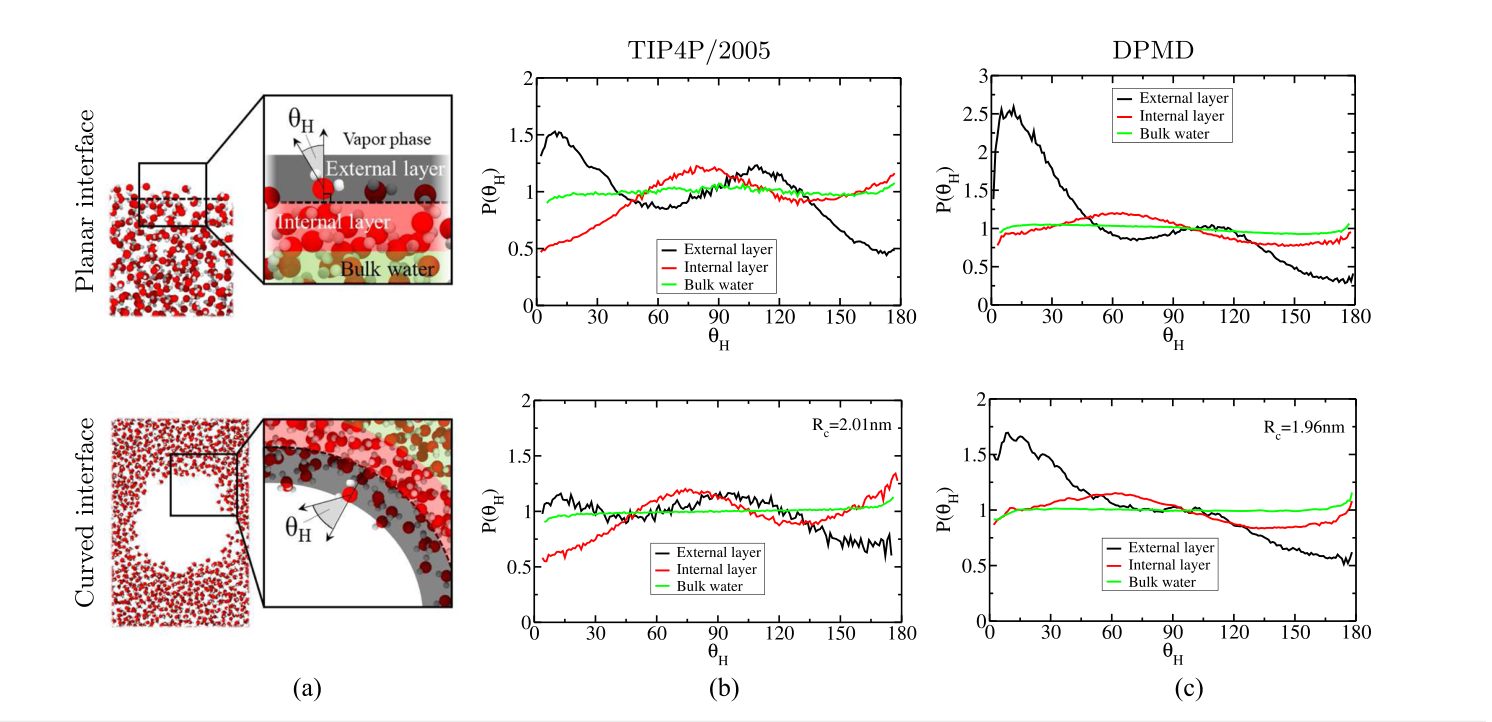
6(a) 包含两个快照,展示了水分子在不同类型的界面的排列。
- 顶部:展示了一个平面界面的板块快照,仅包含少量分子以便于更好的可视化。
- 底部:展示了一个曲面界面的快照。
6(b) 展示了TIP4P/2005模型的归一化直方图,表示在平面和曲面界面的外部区域、内部区域以及体积水中氢键角度θH的分布。
- 顶部:展示了平面界面的θH的直方图。
- 底部:展示了曲面界面的θH的直方图。
6(c) 与6(b)类似,但展示的是DPMD模型的结果,而不是TIP4P/2005模型。
Modular development of deep potential for complex solid solutions (2023年1月16日)
- 作者:Jing Wu, Jiyuan Yang, Li-Yang Ma, Linfeng Zhang, Shi Liu
- 摘要:本文介绍了一种“模块化开发深度势能”(ModDP)的策略,该策略能够系统地开发和改进用于复杂固溶体的深度神经网络模型,即深度势能,几乎不需要人工干预。通过并行学习过程,将与端基材料相关的收敛训练数据库视为独立模块,并重复使用它来训练固溶体的深度势能。ModDP应用于获得两种技术上重要的固溶体Pb$x$Sr${1-x}$TiO$_3$和Hf$x$Zr${1-x}$O$_2$的经典力场。对于这两种材料系统,单一模型能够预测固溶体的各种属性,包括温度驱动和组成驱动的相变。
- PDF链接
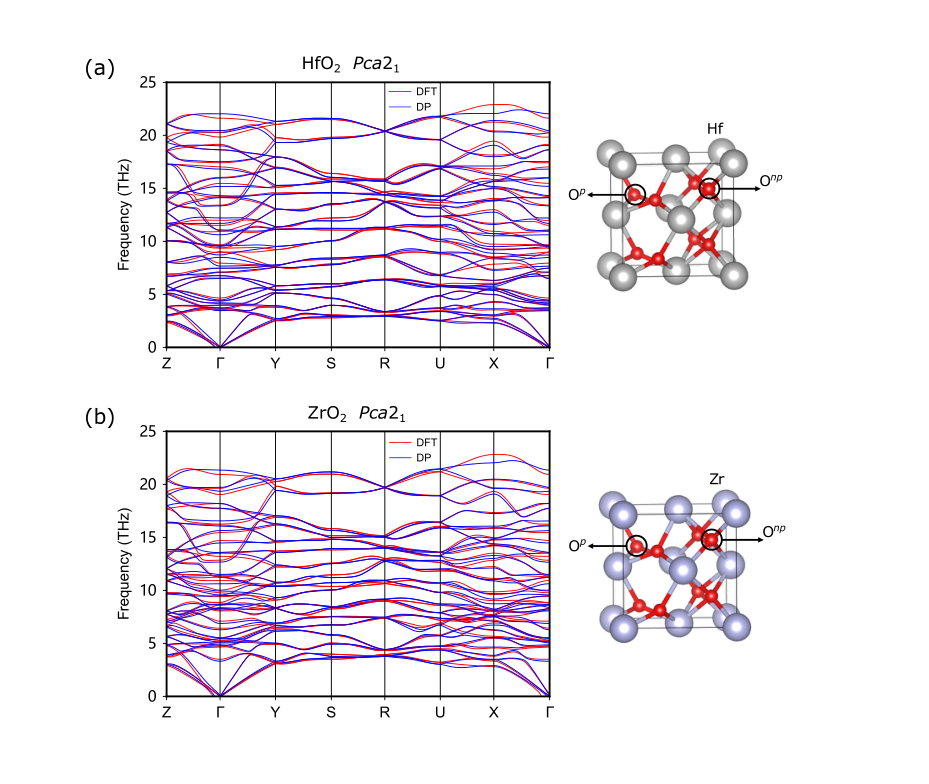
- (a) 展示了Pca21相的分别用
DP和DFT计算得到的HfO2的声子谱。声子谱是一种图表,展示了晶体中原子振动的频率与波数的关系。这有助于理解材料的热和声学性质。 - (b) 展示了Pca21相的ZrO2的声子谱。
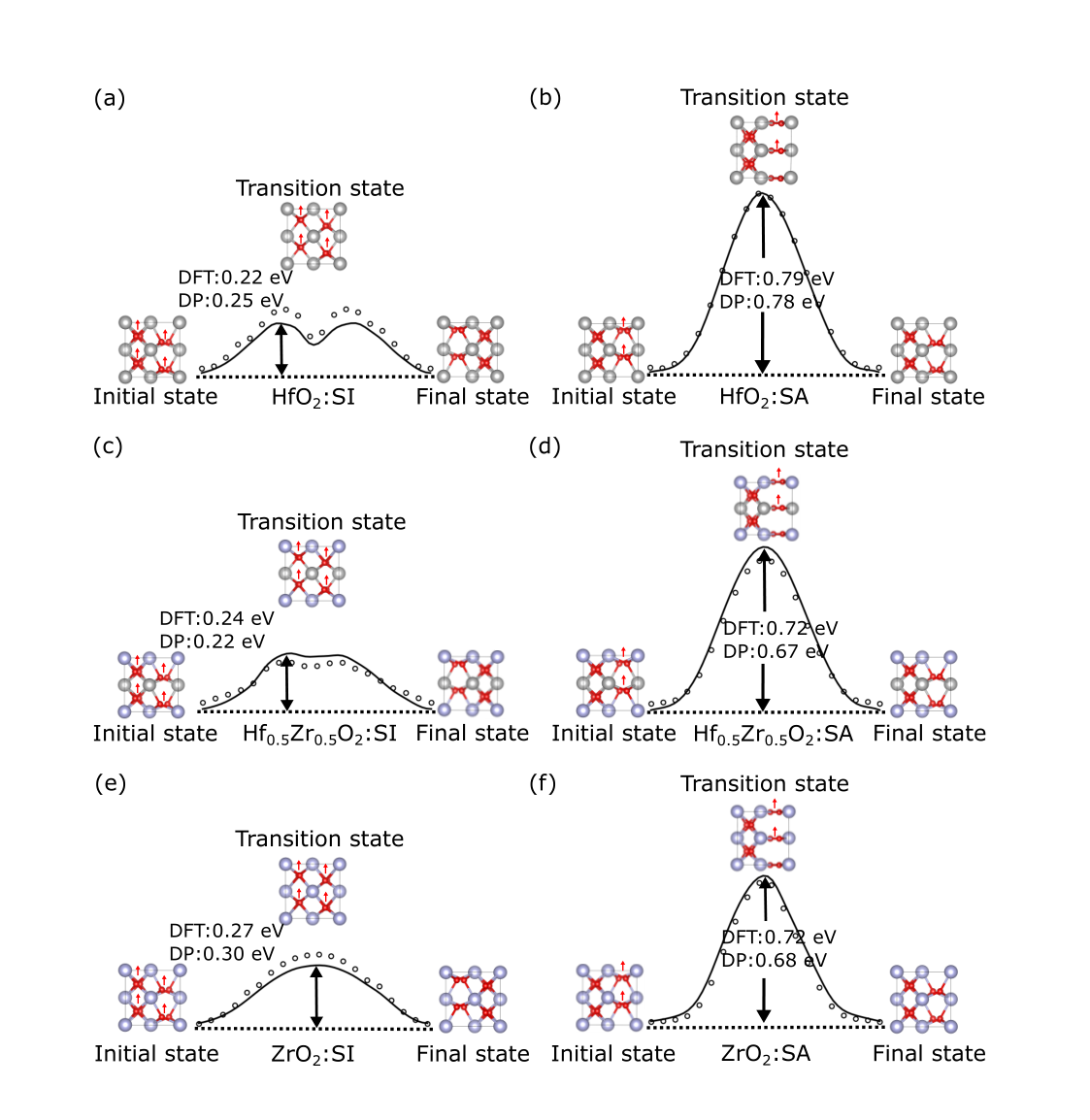
- (a) 展示了HfO2的极化反转的能量障碍的比较。实线表示使用DFT计算的结果,而空心圆表示使用HZO DP模型计算的结果。
- (b) 展示了Hf0.5Zr0.5O2的极化反转的能量障碍的比较。同样,实线表示使用DFT计算的结果,而空心圆表示使用HZO DP模型计算的结果。
- (c) 展示了ZrO2的极化反转的能量障碍的比较。实线和空心圆的表示与上述相同。
可以看出, 基于
DFT和DP计算得到的能带和能量障碍都十分靠近。
找一下其他的分子动力学的神经网络方法
主要关注这些顶会:
- AAAI
- NeulIPS
- ICML
- IJCAI
- ICLR
- WWW
- RTSS
- WINE
论文(中文翻译版本)
作者:Brandon Anderson∗‡, Truong-Son Hy∗ and Risi Kondor∗†]
作者开发了一个名为Cormorant的神经网络架构,专门设计用于学习复杂多体物理系统的行为和性质。这个网络被应用于分子系统,目标是学习用于分子动力学模拟的原子势能面,以及由密度泛函理论计算的分子基态特性。网络的关键特性包括每个神经元明确对应于一组原子子集,每个神经元的激活与旋转是协变的,以确保网络的旋转不变性。此外,网络的非线性基于张量积和Clebsch-Gordan分解,使得网络可以在傅里叶空间中运行。
(2019)
被引用次数:97次
NeurIPS
摘要:我们提出了Cormorant,一个旋转协变神经网络架构,用于学习复杂多体物理系统的行为和性质。
我们将这些网络应用于分子系统有两个目标:学习用于分子动力学模拟的原子势能面,以及学习由密度泛函理论计算的分子基态特性。
我们的网络的一些关键特征是:(a)每个神经元明确对应于一个原子子集;(b)每个神经元的激活与旋转是协变的,确保整个网络是完全旋转不变的。此外,我们的网络中的非线性是基于张量积和ClebschGordan分解,允许网络完全在傅里叶空间中运行。
Cormorant在从MD-17数据集的构象几何中学习分子势能面方面明显优于其他算法,并且在学习GDB-9数据集的分子几何、能量、电子和热力学性质方面与其他方法具有竞争力。
Kondor和Trivedi[2018]给出了傅立叶空间神经网络中允许的操作的完整表征,以保持协方差,Cohen等人将该框架进一步推广到任意规范域[Cohen等人,2019]。最近也有一些研究表明,即使神经网络的非线性部分也是在傅里叶空间中进行的:彼此独立的[Thomas等人,2018]和[Kondor, 2018]首先在旋转协变神经网络中使用Clebsch-Gordan变换来学习物理系统,而[Kondor等人,2018]表明,在球形cnn中,Clebsch-Gordan变换足以作为非线性的唯一来源。
通过这样一种方式建立网络,即每个神经元对应于一组实际的物理原子,并且每次激活都是对称的协变(旋转和平移),我们得到一个网络,其中单个神经元学习的“定律”类似于已知的物理相互作用。
球张量与表示理论
考虑到给定群$G$,$G$的表示$\rho$是一个矩阵值函数$\rho: G \rightarrow \mathbb{C}^{d \times d}$,满足任意两个群元素$x, y \in G$,都有$\rho(x y)=\rho(x) \rho(y)$。很容易看出$\boldsymbol{R}$,以及$\boldsymbol{R} \otimes \ldots \otimes \boldsymbol{R}$是三维旋转群$\mathrm{SO}(3)$的表示。我们也知道,因为$\mathrm{SO}(3)$是一个紧凑群,它有一个可数的单位所谓的不可约表示(irreps)序列,且任何表示都可以通过相似变换简化为不可约表示的直和。在$\mathrm{SO}(3)$的特定情况下,不可约表示被称为Wigner $D$-矩阵,对于任何正整数$\ell=0,1,2, \ldots$,都有一个对应的不可约表示$D^{\ell}(\boldsymbol{R})$,这是一个$(2 \ell+1)$维表示(即,作为函数,$\left.D^{\ell}: \mathrm{SO}(3) \rightarrow \mathbb{C}^{(2 \ell+1) \times(2 \ell+1)}\right)$)。$\ell=0$的不可约表示是平凡的不可约表示$D^0(\boldsymbol{R})=(1)$。
以上意味着存在一个固定的单位变换矩阵$C^{(k)}$,它将$k^{\prime}$阶旋转算子简化为不可约表示的直和:
$$
\underbrace{\boldsymbol{R} \otimes \boldsymbol{R} \otimes \ldots \otimes \boldsymbol{R}}k=C^{(k)}\left[\bigoplus{\ell} \bigoplus_{i=1}^{\tau_{\ell}} D^{\ell}(\boldsymbol{R})\right] C^{(k)^{\dagger}} .
$$
注意,变换$\boldsymbol{R} \otimes \boldsymbol{R} \otimes \ldots \otimes \boldsymbol{R}$包含$D^{\ell}(\boldsymbol{R})$的冗余副本,我们将其表示为多重性$\tau_{\ell}$。对于我们目前的目的,知道$\tau_{\ell}$的实际值并不重要,除了$\tau_k=1$以及对于任何$\ell>k, \tau_{\ell}=0$。重要的是,笛卡尔矩量张量的向量化形式$\bar{T}^{(k)}$有一个对应的分解
$$
\bar{T}^{(k)}=C^{(k)}\left[\bigoplus_{\ell} \bigoplus_{i=1}^{\tau_{\ell}} Q_{\ell, i}\right]
$$
这很好,因为使用$Q_{\ell_i}$的单位性,它表明在旋转下,各个$Q_{\ell, i}$组件独立地变换为$Q_{\ell, i} \mapsto D^{\ell}(\boldsymbol{R}) Q_{\ell, i}$。
我们刚刚描述的是一种应用于旋转下的笛卡尔张量变换的广义傅里叶分析的形式。对于静电多极问题,这尤其相关,因为事实证明,在那种情况下,由于$\bar{T}^{(k)}$的对称性,(4)的唯一非零$Q_{\ell, i}$组件是$\ell=k$的单个组件。此外,对于一组$N$个带电粒子(索引其组件$-\ell, \ldots, \ell) Q_{\ell}$有简单的形式
$$
\left[Q_{\ell}\right]m=\left(\frac{4 \pi}{2 \ell+1}\right)^{1 / 2} \sum{i=1}^N q_i\left(r_i\right)^{\ell} Y_{\ell}^m\left(\theta_i, \phi_i\right) \quad m=-\ell, \ldots, \ell,
$$
其中$\left(r_i, \theta_i, \phi_i\right)$是$i$ ‘th粒子在球坐标中的坐标,$Y_{\ell}^m(\theta, \phi)$是众所周知的球谐函数。$Q_{\ell}$被称为电荷分布的$\ell$ ‘th球状矩。注意,虽然$\bar{T}^{(\ell)}$和$Q_{\ell}$传达完全相同的信息,但$\bar{T}^{(\ell)}$是一个有$3^{\ell}$个组件的张量,而$Q_{\ell}$只是一个$(2 \ell+1)$维向量。
有些混淆的是,在物理和化学中,任何在旋转下变换为$U \mapsto D^{\ell}(\boldsymbol{R}) U$的量$U$通常被称为($\ell$ ‘th阶)球形张量,尽管在其表示方面$Q_{\ell}$只是一个$2 \ell+1$个数字的向量。还要注意,由于$D^0(\boldsymbol{R})=(1)$,零阶球形张量只是一个标量。另一方面,一阶球形张量可以用来表示空间向量$\boldsymbol{r}=(r, \theta, \phi)$,通过设置$\left[U_1\right]_m=r Y_1^m(\theta, \phi)$。
总体神经网络构造:
除了上述的协变神经元,我们的网络还需要神经元来计算输入特征化和协变层后的最终输出。因此,总的来说,Cormorant网络包括三个不同的部分:
一个输入特征化网络$\left{F_j^{s=0}\right} \leftarrow \operatorname{INPUT}\left(\left{Z_i, r_{i, j}\right}\right)$,只对原子电荷/身份和(可选的)相对位置$r_{i, j}$的标量函数进行操作。
一个$S$-层协变激活$F_i^s$的网络$\left{F_i^{s+1}\right} \leftarrow \operatorname{CGNet}\left(\left{F_i^s\right}\right)$,每个激活都是类型为$\tau_i^s$的$\mathrm{SO}(3)$-向量。
顶部的旋转不变网络$y \leftarrow \operatorname{OUTPUT}\left(\bigoplus_{s=0}^S\left{F_i^s\right}\right)$,它从激活$F_i^s$构造标量,并用它们来预测回归目标$y$。
我们将输入和输出特征化的细节留给补充材料。
Cormorant和其他最近的协变网络(Tensor Field Networks [Thomas et al., 2018] 和 SE(3)-equivariant networks [Weiler et al., 2018])的一个关键区别是使用Clebsch-Gordan非线性。Clebsch-Gordan非线性导致激活中每个自由度的完全交互。这增加了训练的难度,如补充材料中所讨论的。我们进一步指出,SE(3)-equivariant网络使用三维点网格来表示数据,并确保每层的平移和旋转协变性(等价性)。另一方面,Cormorant使用的激活对旋转是协变的,对平移是严格不变的。
实验结果
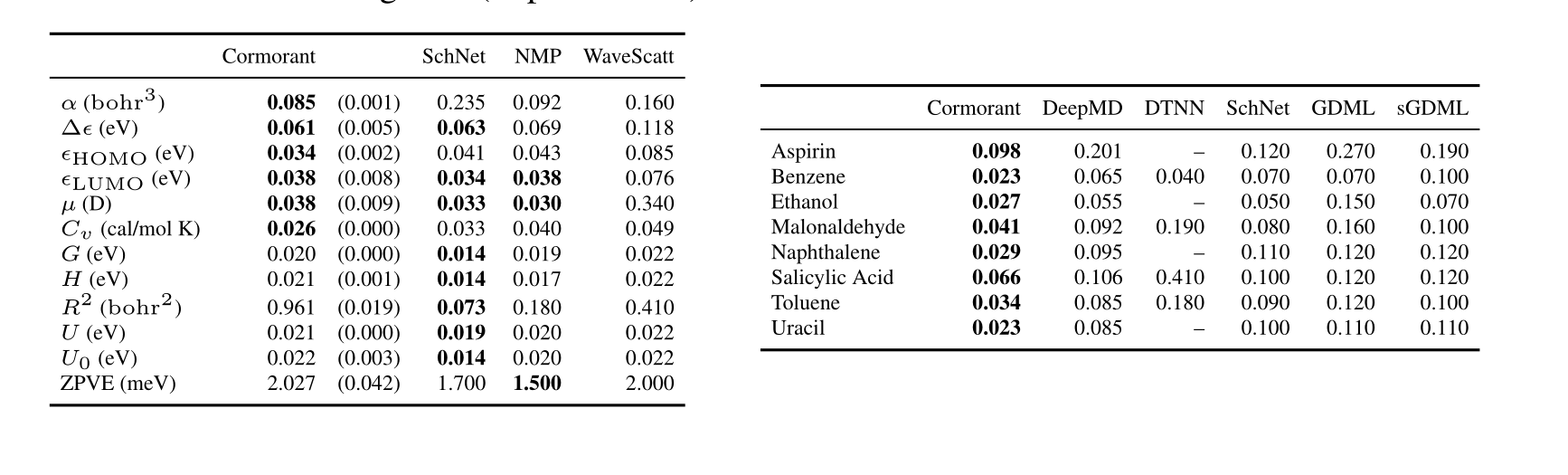
实验结果是在两个对计算化学社区感兴趣的数据集上进行的:MD-17用于学习分子力场和势能表面,QM-9用于学习一组分子的基态性质。他们的代码已经在GitHub上公开。
QM9数据集包含约134k个小有机分子,包含H、C、N、O、F等原子。对于每个分子,使用密度泛函理论(DFT)计算基态配置以及各种分子性质。他们使用基态配置作为Cormorant的输入,并使用文献中的常见子集作为回归目标。他们的结果与SchNet、MPNNs和wavelet scattering networks进行了比较。在考虑的十二个回归目标中,他们在六个目标上取得了领先或有竞争力的结果。
MD-17数据集包含八个小有机分子,包含最多17个总原子,由H、C、N、O、F等原子组成。对于每个分子,使用DFT运行一个从头算的分子动力学模拟以计算基态能量和力。在间歇时间步,记录能量、力和配置(每个原子的位置)。对于每个分子,他们使用50k/10k/10k原子的训练/验证/测试划分。他们的实验结果显示,Cormorant网络在所有竞争者中表现最好。
总的来说,据他们所知,Cormorant是第一个神经网络架构,其中神经元实现的操作直接由已知的物理相互作用的形式激发。旋转和平移不变性明确地“烘焙到”网络中,因为所有激活都以球形张量形式(SO(3)–向量)表示,神经元结合Clebsch–Gordan乘积,部分的串联和与可学习权重的混合,所有这些都是协变操作。在未来的工作中,他们设想Cormorant学习的势能将直接集成在MD模拟框架中。在这方面,非常鼓舞人心的是,在MD-17上,这是力场学习的标准基准,Cormorant超过了所有其他竞争方法。从导数(力)学习和推广到其他紧凑对称群是这项工作的自然扩展。
github链接:https://github.com/risilab/cormorant/
神经网络结构:
class CatMixReps(CGModule):
"""
Module to concatenate mix a list of representation representations using
:obj:`cormorant.nn.CatReps`, and then linearly mix them using
:obj:`cormorant.nn.MixReps`.
Parameters
----------
taus_in : List of :obj:`SO3Tau` (or compatible object).
List of input tau of representation.
tau_out : :obj:`SO3Tau` (or compatible object), or :obj:`int`.
Input tau of representation. If an :obj:`int` is input,
the output type will be set to `tau_out` for each
parameter in the network.
maxl : :obj:`bool`, optional
Maximum weight to include in concatenation.
real : :obj:`bool`, optional
Use purely real mixing weights.
weight_init : :obj:`str`, optional
String to set type of weight initialization.
gain : :obj:`float`, optional
Gain to scale initialized weights to.
device : :obj:`torch.device`, optional
Device to initialize weights to.
dtype : :obj:`torch.dtype`, optional
Data type to initialize weights to.
"""
def __init__(self, taus_in, tau_out, maxl=None,
real=False, weight_init='randn', gain=1,
device=None, dtype=None):
super().__init__(device=device, dtype=dtype)
self.cat_reps = CatReps(taus_in, maxl=maxl)
self.mix_reps = MixReps(self.cat_reps.tau, tau_out,
real=real, weight_init=weight_init, gain=gain,
device=device, dtype=dtype)
self.taus_in = taus_in
self.tau_out = SO3Tau(self.mix_reps)
def forward(self, reps_in):
"""
Concatenate and linearly mix a list of representations.
Parameters
----------
reps_in : :obj:`list` of :obj:`list` of :obj:`torch.Tensors`
List of input representations.
Returns
-------
reps_out : :obj:`list` of :obj:`torch.Tensors`
Representation as a result of combining and mixing input reps.
"""
reps_cat = self.cat_reps(reps_in)
reps_out = self.mix_reps(reps_cat)
return reps_out
@property
def tau(self):
return self.tau_out
图神经网络的介绍
图层次的问题
定点层次的问题
边层次的问题
A Gentle Introduction to Graph Neural Networks (distill.pub)
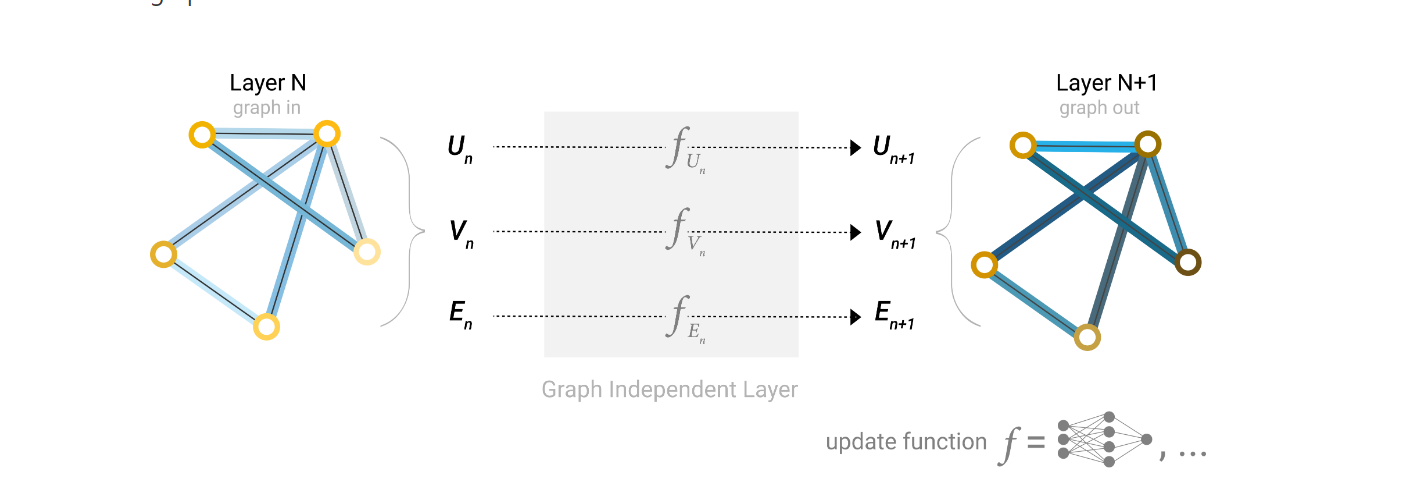
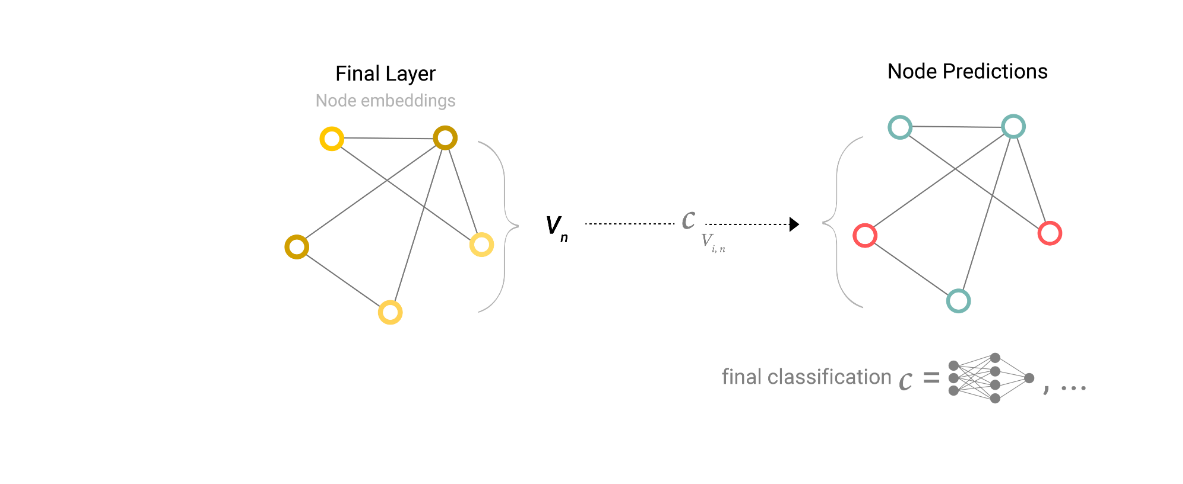
所有节点共享一个MLP。
如果一个节点没有向量表示, 想得到他的向量->pooling
- 拿出和他连接的边的向量
- 拿出全局的向量
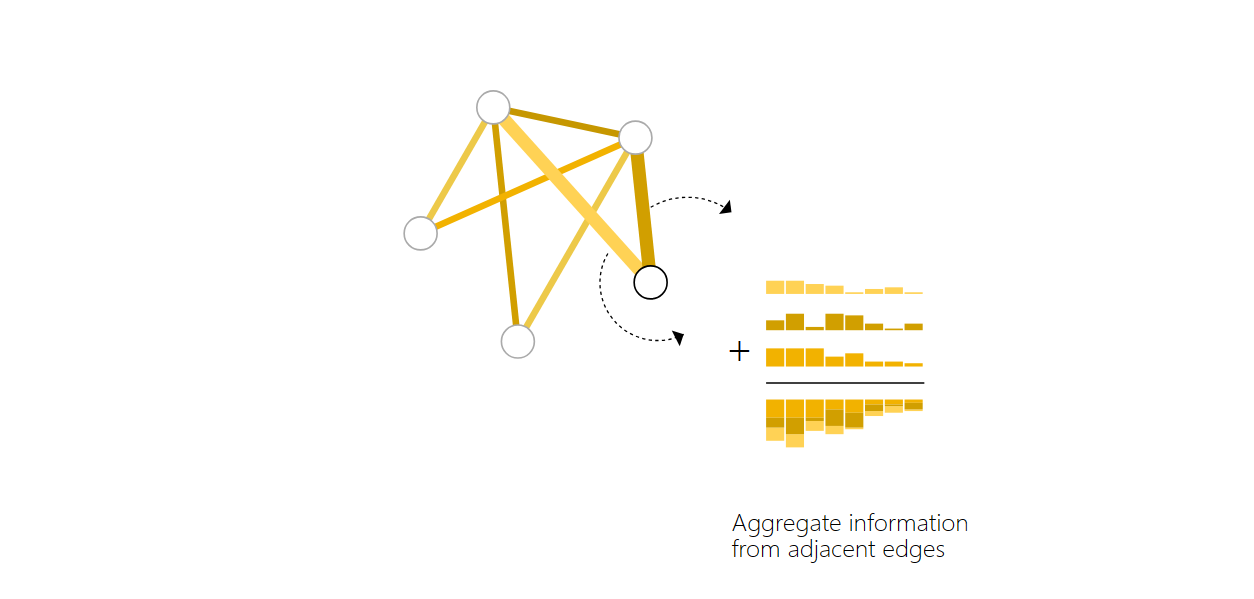
- 加上面的向量加起来,(如果维度不一样,需要做一个投影)
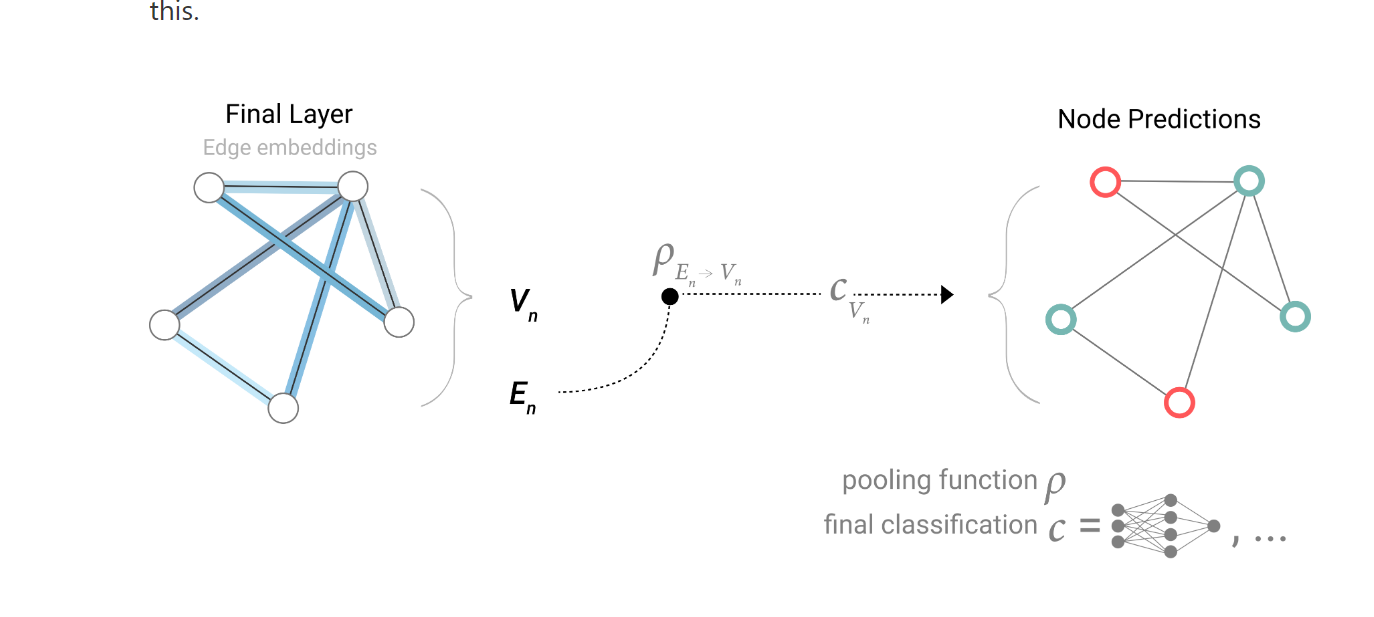
同样的,如果是边没有向量,也可以做相同的pooling, 如果没有全局向量,就把所有的边/节点的向量加起来。
总体来说,一个GNN长这样:

信息传递:
获得一个节点的向量时, 取其所有的邻居向量然后加和,再传入MLP。类似于做CNN里面的卷积,但是这里面的卷积的权重是一样的。
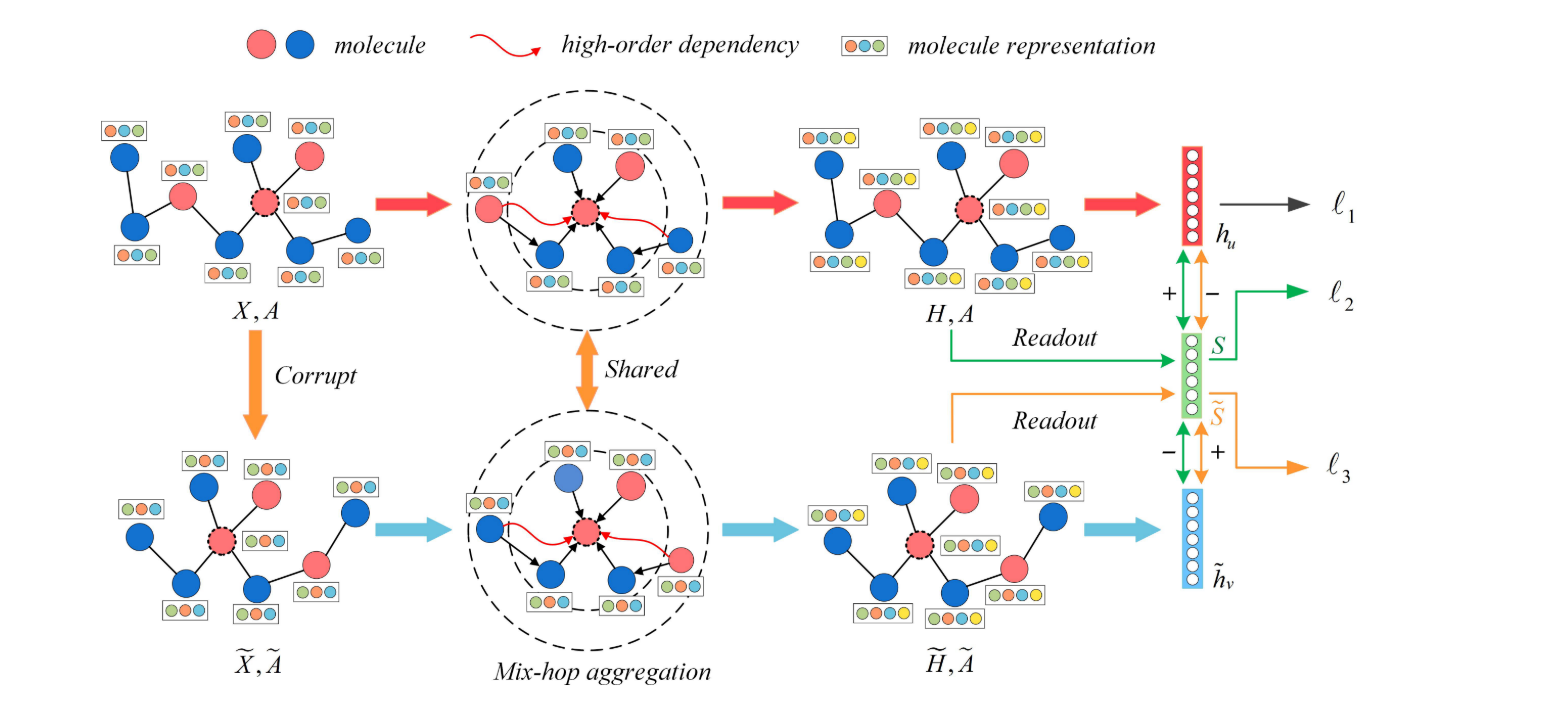
学习神经生成动力学用于分子构象生成(CSGNN) 作者:Ziyao Li, Qiang Liu 和 Jian Peng
本文提出了一种结合流基模型和能量基模型优点的方法,用于生成分子构象。 (2021)
- 作者:Ziyao Li, Qiang Liu 和 Jian Peng
- 被引用次数:2次
- IJCAI
- 摘要:分子构象生成是计算化学中的重要任务,应用于药物发现和材料设计。现有的方法要么依赖于流基模型,这些模型学习潜在空间和构象空间之间的确定性转换,要么依赖于能量基模型,这些模型学习潜在能量函数以指导构象采样。然而,流基模型通常无法捕获分子构象的复杂多模态分布,而能量基模型通常受到收敛速度慢和可扩展性差的困扰。在本文中,我们提出了神经生成动力学(NGD),这是一个新颖的框架,它结合了流基模型和能量基模型的优点,用于分子构象生成。NGD学习了一个定义潜在空间中连续时间随机动力学的神经常微分方程(ODE),以及潜在空间和构象空间之间的可逆映射。通过模拟潜在动力学并将潜在状态转换到构象空间,NGD可以生成多样化和逼真的分子构象。我们在几个分子构象生成的基准测试上评估了NGD,并显示出它在生成构象的多样性、真实性和效率方面超过了现有的方法。
- PDF链接
问题抽象:
A molecular interaction network can be viewed as an undirected attributed graph $\mathcal{G}=(\mathcal{V}, \mathcal{E}, \boldsymbol{X})$, where $\mathcal{V}$ represents the set of nodes that correspond to molecular entities (e.g., drugs, diseases or proteins) and $\mathcal{E} \subseteq \mathcal{V} \times \mathcal{V}$ denotes the set of edges indicating the existence of interaction between two entities in $\mathcal{V} . \boldsymbol{X} \in \mathbb{R}^{|\mathcal{V}| \times m}$ is a feature matrix where each node in $\mathcal{V}$ is encoded as a predefined $m$-dimensionality attribute vector (e.g., a generated graph embedding or a one-hot coding). Specifically, the graph can be further represented as an adjacency matrix $\boldsymbol{A} \in{0,1}^{|\mathcal{V}| \times|\mathcal{V}|}$ where $\boldsymbol{A}{u, v}=1$ if there exists a link from $u$ to $v$ in the graph (i.e., $(u, v) \in \mathcal{E}$ ) and $\boldsymbol{A}{u, v}=0$ otherwise. Note that $\mathcal{G}$ is a undirected graph, hence, $\boldsymbol{A}$ is symmetric. Our goal of molecular interaction prediction is to learn a mapping function $\Theta(\omega): \mathcal{E} \rightarrow[0,1]$ from edges to scores, where $\omega$ is parameter, such that we can obtain the probability that two arbitrary nodes interact each other [Huang et al., 2020b].
数据集:
(1)ChG-Miner由5,018种药物组成,通过15,139种药物-靶标相互作用(DTI)靶向2,325种蛋白质。(2)ChChMiner包含1,514种药物之间的48,514种相互作用(3)HuRI-PPI包括HI-III网络中5,604种蛋白质(PPI)之间的23,322种相互作用。(4)DG-AssocMiner包括519种疾病,通过2,1357个关联(DGI)关联7,294个基因。(5)DD-Miner是一个数据集,包含6,878种疾病(DIA)之间的6,877种关联(6)DCh-Miner包含5,536种疾病,通过466,657种关联(DDA)与1,663种药物相关。(7)ChSe-Decagon包括639种药物,10,184种副作用和其中的17,499种协会(DSA)。我们从BioSNAP下载DTI、DDI、DGI、DIA、DDA和DSA [Marinka Zitnik和Leskovec,2018],并从CCSB收集PPI [Luck等人,2020年]。详细信息见表1。

BenchMark
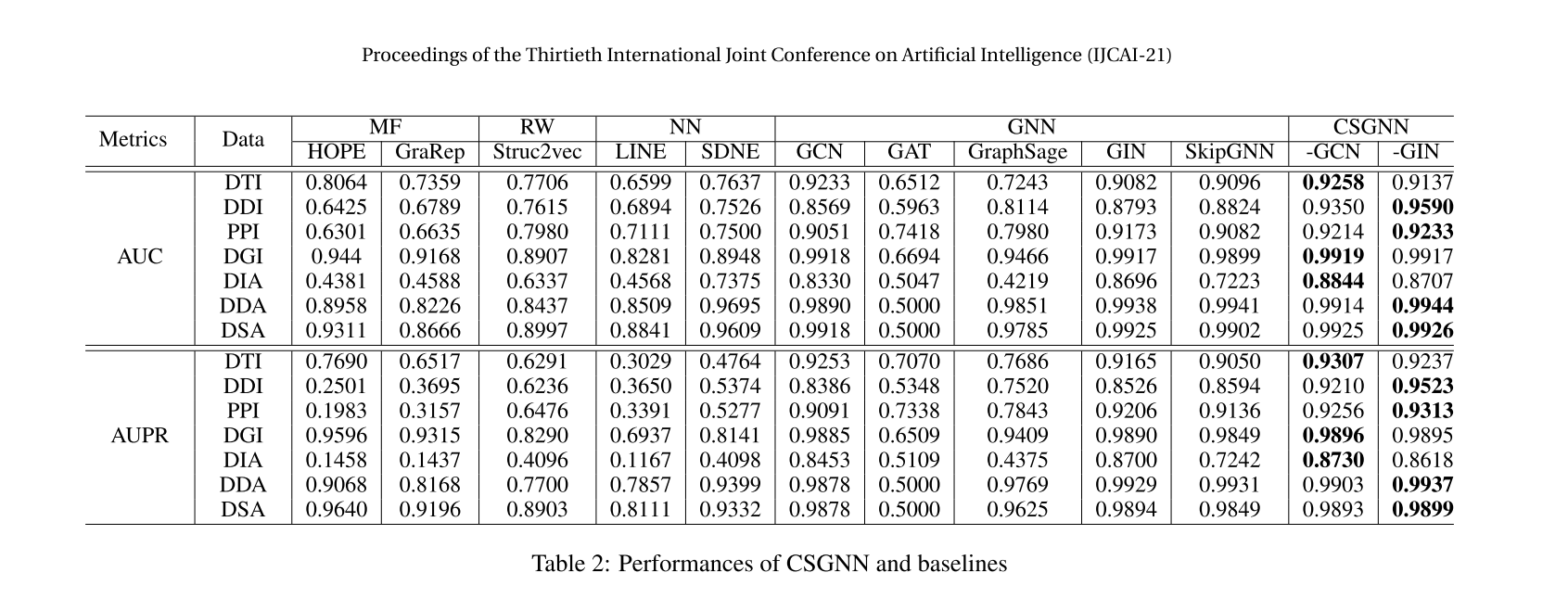
可以参考使用了GNN的论文:
• Graph Neural Network (GNN) considers both topological information and node and/or edge information in graph. Several most representative GNN-based methods including GCN [Kipf and Welling, 2017], GAT [Velickovic et al., 2018], GraphSage [Hamilton et al., 2017], GIN [Xu et al., 2019a] and SkipGNN [Huang et al., 2020b] are selected.
神经消息传递与边缘更新用于预测分子和材料的性质 作者:Peter Bjørn Jørgensen, Karsten Wedel Jacobsen 和 Mikkel Nørgaard Schmidt
本文引入了一种新的神经消息传递方案,该方案更新节点和边缘特征,并将其应用于预测分子和材料的性质。
(2020)
- 作者:Peter Bjørn Jørgensen, Karsten Wedel Jacobsen 和 Mikkel Nørgaard Schmidt
- 被引用次数:48次
- IJCAI
- 摘要:神经消息传递(NMP)模型在预测结构化数据(如分子和材料)的性质方面显示出了巨大的潜力。然而,大多数现有的NMP模型只更新节点特征,而保持边缘特征固定,这限制了它们捕获节点间交互动态变化的能力。在本文中,我们提出了一种新的NMP方案,通过使用两种类型的消息:节点到边缘和边缘到节点,同时更新节点和边缘特征。我们展示了我们的模型可以有效地从
- 节点和边缘属性中学习,并通过自我注意机制整合全局信息。我们将我们的模型应用于预测分子和材料的性质的几个任务,如分子能量、溶解度、毒性、形成能和带隙。实验结果表明,我们的模型在几个基准测试上达到了最先进的性能,而消融研究证实了边缘更新和自我注意对改善模型性能的重要性。
- PDF链接
目标
简而言之,性质预测的关键思想是首先将输入分子m映射到具有表示函数h = g(m)的密集特征向量,然后基于y = f(h)的嵌入来预测目标性质。
然而,基于描述符的表示方法假设与任务预测相关的所有信息都覆盖在所选择的描述符集中,限制了模型学习现有化学知识的能力。
MPNN框架包括三个主要模块:
(1)消息传递模块,其中,每个原子的信息从其邻居跨分子图传递到消息向量中;(2)更新模块,其中基于所获得的消息向量来更新分子中的每个原子处的隐藏状态;
主要贡献:
我们提出了一个基于有向图的通信消息传递神经网络,一个有效的图形模型,以更新的边缘和节点嵌入交互式。
引入消息助推器以丰富消息生成过程,其可以推广到其他与图相关的任务,例如节点分类和链接预测。
在不同级别的公共数据集上进行了大量的实验,以证明我们的方法的有效性。
$$
\begin{array}{l|l}
\hline G=(V, E) & \text { Input graph. } \
\hline u, v, \ldots & \text { Nodes in } G . \
\hline \mathbf{e}{u, v} & \text { A link from node } u \text { to } v . \
\hline N(v) & \text { The set of neighbor nodes of node } v . \
\hline \mathbf{x} & \text { Raw feature. } \
\hline \mathbf{h}^i(v) & \begin{array}{l}
\text { The hidden representation of node } v \text { in } \
\text { layer } i .
\end{array} \
\hline \mathbf{h}^i\left(\mathbf{e}{v, w}\right) & \begin{array}{l}
\text { The hidden representation of edge } \mathbf{e}_{v, w} \text { in } \
\text { layer } i .
\end{array} \
\hline \mathbf{W} & \text { Weight matrix. } \
\hline \sigma & \text { Acitive function. } \
\hline
\end{array}
$$


信息传递增强

节点和边的信息交流

数据集

benchmark