DeepMD详细内容介绍

2023/7/2

DeePMD 调研报告

简介
背景和动机
DeePMD-kit 概述
核心算法
代码实现和网络架构
图神经网络在 DeePMD 中的应用
应用案例
性能评估
与其他工具的比较
社区和资源
未来展望
结论
参考文献

简介

背景介绍

分子动力学（MD）模拟在凝聚态物理、材料科学、聚合物化学和分子生物学等领域具有广泛的应用，它允许研究人员检查原子或分子的行为，这在实验难以进行时尤为宝贵。然而，MD模拟的质量受到势能（PES）准确性的限制。传统上，有两种常见的模型：经验性原子势模型和量子力学模型。经验性原子势模型在计算上高效但准确性有限，而量子力学模型虽然准确度高，但计算成本很高。近年来，机器学习（ML）模型开始崭露头角，用于解决准确性和效率之间的权衡问题。ML模型通过训练来建立原子配置和势能之间的关系，并能达到与量子力学方法相当的准确性，同时具有更低的计算成本。深度势（DP）模型是ML模型的一种，它不仅具有量子力学精度，而且具有高计算效率，并且是端到端的，支持在现代高性能计算机上高效运行。

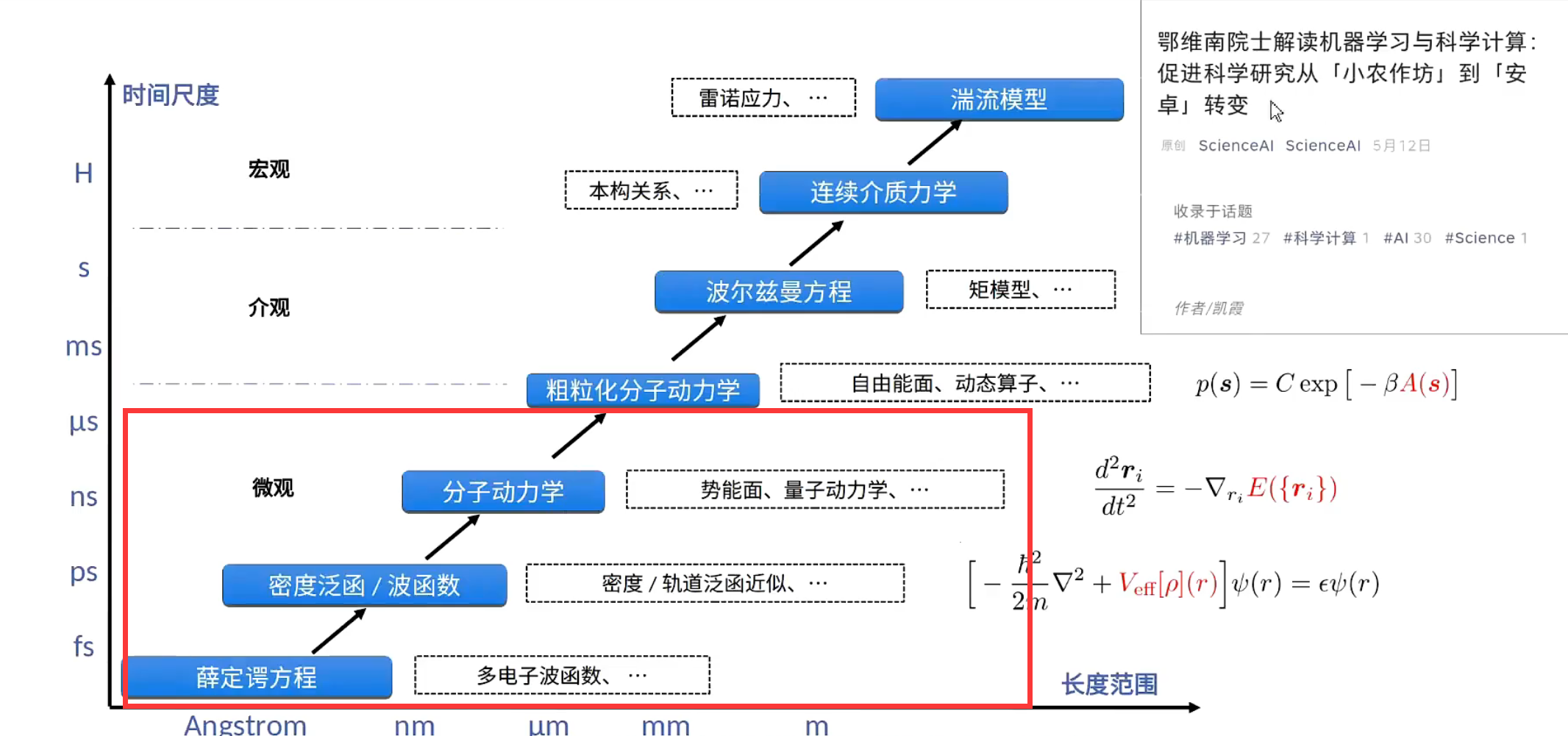
DeePMD-kit 概述

DeePMD-kit 是一个使用深度学习模型来高效模拟分子动力学的工具包。下面是相关的参考内容：

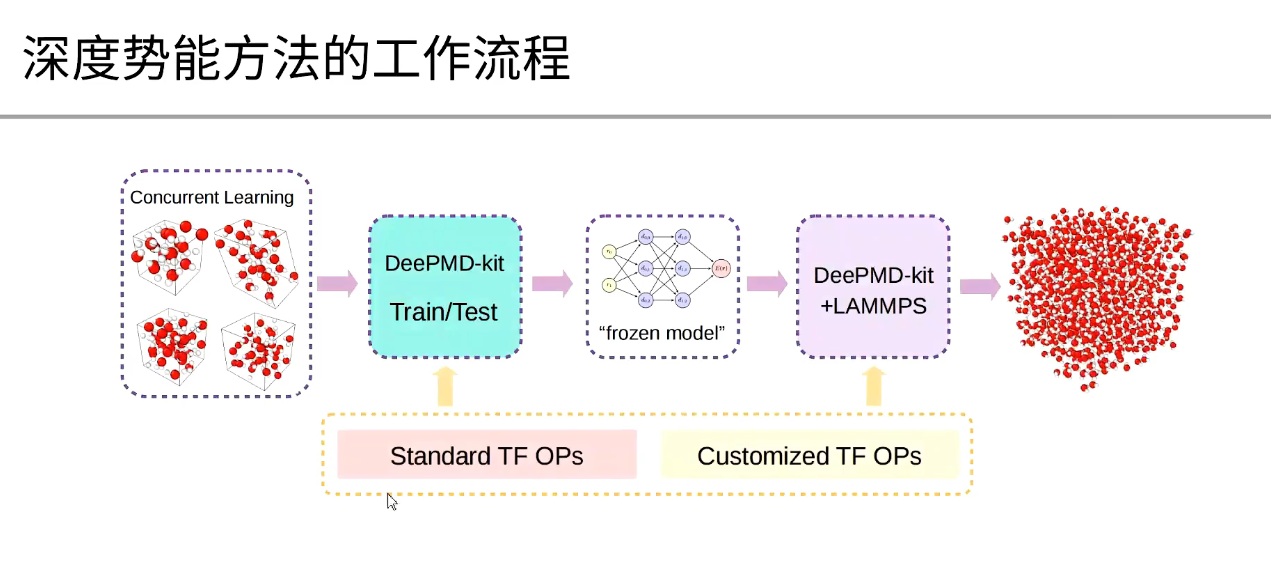
DeePMD-kit 的工作流程

准备训练数据：从量子力学模拟收集原子配置和相应的能量和力。
配置 DeePMD-kit：创建输入文件，指定训练数据、神经网络结构和训练参数。
描述符生成：DeePMD-kit 使用局部环境矩阵 $ \mathcal{R} $，它描述了特定原子及其邻居之间的距离和方向向量。
嵌入网络：将每个距离嵌入到 $ M_1 $ 维向量中，从而将环境矩阵 $ \mathcal{R} $ 嵌入到矩阵 $ \mathcal{G} $ 中。
拟合网络：通过矩阵乘法从 $ \mathcal{G} $ 中提取描述符向量，然后将描述符输入到拟合网络以获得预测能量。
原子类型嵌入：DeePMD-kit v2.0 允许在不同原子类型之间共享嵌入网络和拟合网络，从而降低训练复杂性。

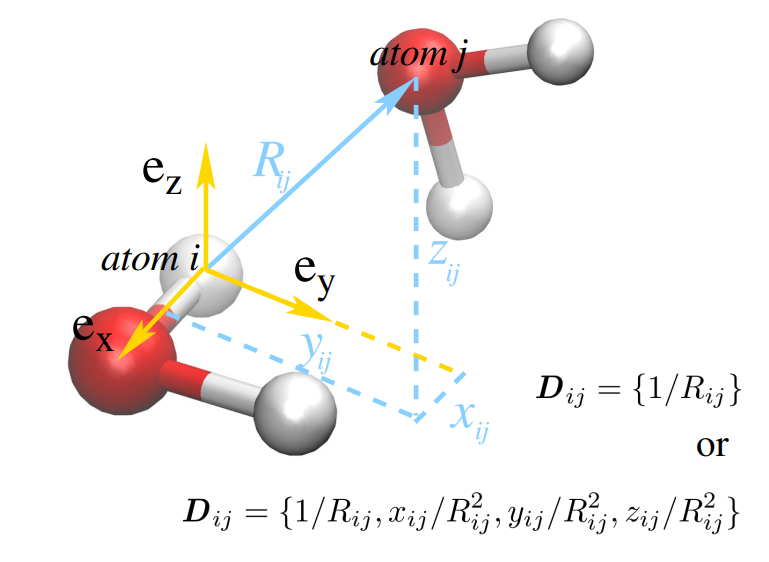
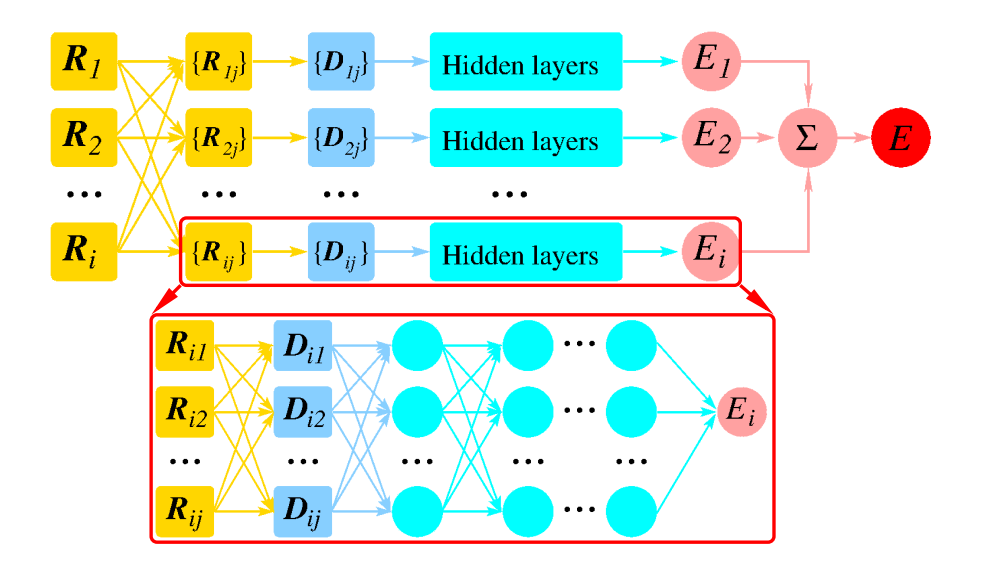
DeePMD-kit 的原理

理论基础

在介绍DP方法之前，我们定义了一个包含N个原子的系统的坐标矩阵$\mathcal{R} \in \mathbb{R}^{N \times 3}$，

$\mathcal{R}=\left{\boldsymbol{r}_1^T, \cdots, \boldsymbol{r}_i^T, \cdots, \boldsymbol{r}_N^T\right}^T, \boldsymbol{r}_i=\left(x_i, y_i, z_i\right),(1)$

$\boldsymbol{r}i$包含原子$i$的3个笛卡尔坐标，$\boldsymbol{\mathcal { R }}$可以转换为局部环境矩阵$\left{\boldsymbol{\mathcal { R }}^i\right}{i=1}^N$

$\mathcal{R}^i=\left{\boldsymbol{r}{1 i}^T, \cdots, \boldsymbol{r}{j i}^T, \cdots, \boldsymbol{r}{N_i, i}^T\right}^T, \boldsymbol{r}{j i}=\left(x_{j i}, y_{j i}, z_{j i}\right),(2)$

其中$j$和$N_i$是原子$i$在截止半径$r_c$内的邻居的索引，$\boldsymbol{r}_{j i} \equiv \boldsymbol{r}_j-\boldsymbol{r}_i$被定义为相对坐标。
在DP方法中，系统的总能量$E$被构造为原子能量的总和。

$E=\sum_i E_i,(3)$

其中$E_i$是原子$i$的局部原子能量。$E_i$取决于原子$i$的局部环境：

$E=\sum_i E_i=\sum_i E\left(\mathcal{R}^i\right),(4)$

$\mathcal{R}^i$到$E_i$的映射分两步构造。如下图所示，

首先，$\mathcal{R}^i$被映射到一个特征矩阵，也称为描述符，$\mathcal{D}^i$，以保持系统的平移、旋转和排列对称性。$\mathcal{R}^i \in \mathbb{R}^{N_i \times 3}$首先被转换为广义坐标$\tilde{\mathcal{R}}^i \in \mathbb{R}^{N_i \times 4}$。

$\left{x_{j i}, y_{j i}, z_{j i}\right} \mapsto\left{s\left(r_{j i}\right), \hat{x}{j i}, \hat{y}{j i}, \hat{z}_{j i}\right}$

其中$\hat{x}{j i}=\frac{s\left(r{j j}\right) x x_{j i}}{r_{j i}}, \hat{y}{j i}=\frac{s\left(r{j j}\right) y \ddot{j}}{r_{j i}}$, 和 $\hat{z}{j i}=\frac{s\left(r{j j}\right) z j i}{r_{j i}}$。$s\left(r_{j i}\right)$是一个权重函数，用于减少离原子$i$较远的粒子的权重，定义为：

$s\left(r_{j i}\right)= \begin{cases}\frac{1}{r_{j i}}, & r_{j i}<r_{c s} \ \frac{1}{r_{j i}}\left{\left(\frac{r_{j i}-r_{c s}}{r_c-r_{c s}}\right)^3\left(-6\left(\frac{r_{j j}-r_{c s}}{r_c-r_{c s}}\right)^2+15 \frac{r_{j j}-r_{c s}}{r_c-r_{c s}}-10\right)+1\right}, & r_{c s}<r_{j i}<r_c,(6) \ 0, & r_{j i}>r_c\end{cases}$

这里$r_{j i}$是原子$i$和$j$之间的欧几里得距离，$r_{c s}$是平滑截止参数。通过引入$s\left(r_{j i}\right)$，$\tilde{\mathcal{R}}^i$中的分量从$r_{c s}$到$r_c$平滑地变为零。然后，$s\left(r_{j i}\right)$，即$\tilde{\mathcal{R}}^i$的第一列，通过嵌入神经网络映射到嵌入矩阵$\mathcal{G}^{i 2} \in \mathbb{R}^{N_i \times M_1}$。通过取$\mathcal{G}^{i 2} \in \mathbb{R}^{N_i \times M_2}$的前$M_2\left(<M_1\right)$列，我们得到另一个嵌入矩阵$\mathcal{G}^{i 2} \in \mathbb{R}^{N_i \times M_2}$。最后，我们定义原子$i$的特征矩阵$\mathcal{G}^{i 2} \in \mathbb{R}^{M_1 \times M_2}$：

$\mathcal{D}^i=\left(\mathcal{G}^{i 1}\right)^T \tilde{\mathcal{R}}^i\left(\tilde{\mathcal{R}}^i\right)^T \mathcal{G}^{i 2},(7)$

在特征矩阵中，通过$\tilde{\mathcal{R}}^i\left(\tilde{\mathcal{R}}^i\right)^T$的矩阵乘积保持平移和旋转对称性，并通过$\left(\mathcal{G}^i\right)^T \tilde{\mathcal{R}}^i$的矩阵乘积保持排列对称性。接下来，每个$\mathcal{D}^i$通过拟合网络映射到局部原子能量$E_i$。

嵌入网络$\mathcal{N}^e$和拟合网络$\mathcal{N}^f$都是包含几个隐藏层的前馈神经网络。从前一层的输入数据$d_l^{\text {in }}$到下一层的输出数据$d_k^{\text {out }}$的映射由线性和非线性变换组成。

$d_k^{o u t}=\varphi\left(\sum_{k l} w_{k l} d_l^{i n}+b_k\right),(8)$

在等式(8)中，$w_{k l}$是连接权重，$b_k$是偏置权重，$\varphi$是非线性激活函数。需要注意的是，只在输出节点应用线性变换。嵌入和拟合网络中包含的参数是通过最小化损失函数$L$获得的：

$L\left(p_\epsilon, p_f, p_{\xi}\right)=\frac{p_\epsilon}{N} \Delta \epsilon^2+\frac{p_f}{3 N} \sum_i\left|\Delta \boldsymbol{F}i\right|^2+\frac{p{\xi}}{9 N}|\Delta \xi|^2,(9)$

其中$\Delta \epsilon, \Delta \boldsymbol{F}i$, 和 $\Delta \xi$分别表示能量、力和应力的均方根误差。在训练过程中，前因子$p_\epsilon, p_f$, 和 $p{\xi}$由以下公式确定

$p(t)=p^{\operatorname{limit}}\left[1-\frac{r_l(t)}{r_l^0}\right]+p^{\operatorname{start}}\left[\frac{r_l(t)}{r_l^0}\right]$

其中$r_l(t)$和$r_l^0$分别是训练步骤$t$和训练步骤0的学习率。$r_l(t)$定义为

$r_l(t)=r_l^0 \times d_r^{t / d_s}$

其中$d_r$和$d_s$分别是衰减率和衰减步骤。衰减率$d_r$需要小于1。有关DeepPot-SE (DP)方法的详细信息，请参阅原始论文。

分子动力学

分子动力学模拟是一种从微观出发的模拟手段，在科学发现，工程设计等领域具有重要作用。

$\begin{aligned}
& m_i \frac{d^2 \boldsymbol{r}_i}{d t^2}=-\nabla_i E \
& E=E\left(\boldsymbol{r}_1, \boldsymbol{r}_2, \ldots, \boldsymbol{r}_N\right)
\end{aligned}$

计算能量的常见的方式

方法	例子	优缺点
第一性原理计算密度泛函理论(DFT)	密度泛函理论(DFT)	精度高，计算复杂度高
计算经验力场	LJ，EAM，MEAM	计算复杂度低，精度不可靠

DeePKS（电子结构）

满足要求比较好的是单电子的密度矩阵，然后把波函数投影到一组比较好的完备基上。

构建过程

给定原子坐标，写出电子结构，利用DFT计算得到能量，构建坐标能量对，典型的监督学习，回归问题。
利用DNN来构建体系坐标和能量的关系。

常见的问题：
- 物理约束（旋转性，对称性，平移，交换…）

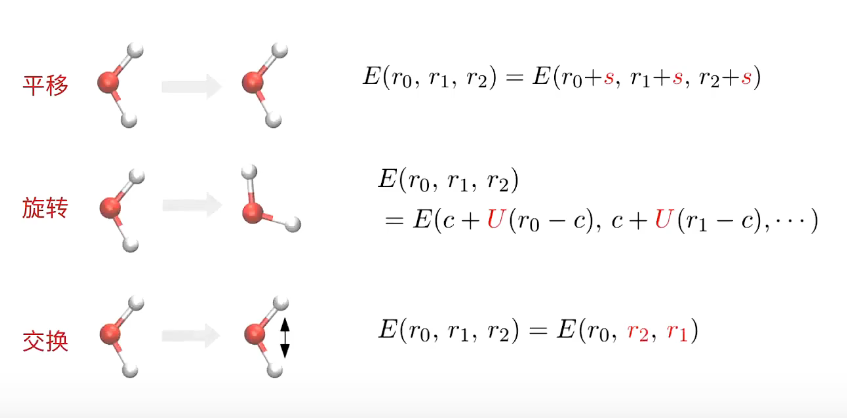
小原子数量训练得到的在大体系上是否存在问题？
深度势能的构建关系
$
E=\sum_i \mathcal{N}{\alpha_i}\left(\mathcal{D}{\alpha_i}\left(r_i,\left{r_j\right}_{j \in n(i)}\right)\right)
$

Function $f\left(x_1, x_2, \ldots x_N\right)$ is permutationally invariant if and only if there exist $\rho$ and $\phi$ such that $f\left(\left{x_i\right}\right)=\rho\left(\sum_i \phi\left(x_i\right)\right)$
$
\mathcal{R}i=\left(\begin{array}{cccc}
1 / r{i 1} & x_{i 1} / r_{i 1}^2 & y_{i 1} / r_{i 1}^2 & z_{i 1} / r_{i 1}^2 \
1 / r_{i 2} & x_{i 2} / r_{i 2}^2 & y_{i 2} / r_{i 2}^2 & z_{i 2} / r_{i 2}^2 \
1 / r_{i 3} & x_{i 3} / r_{i 3}^2 & y_{i 3} / r_{i 3}^2 & z_{i 3} / r_{i 3}^2 \

\vdots & \vdots & \vdots & \vdots
\end{array}\right) \
\mathcal{G}_i=\left(\begin{array}{cccc}

G_1\left(r_{i 1}\right) G_2\left(r_{i 1}\right) & G_3\left(r_{i 1}\right) & \cdots \
G_1\left(r_{i 2}\right) & G_2\left(r_{i 2}\right) & G_3\left(r_{i 2}\right) & \cdots \
G_1\left(r_{i 3}\right) & G_2\left(r_{i 3}\right) & G_3\left(r_{i 3}\right) & \cdots \
\vdots & \vdots & \vdots & \ddots
\end{array}\right)
$

R：环境矩阵，对于每一个原子来说的，元素是原子之间的相对距离，所以满足平移相对性，

G： embedding matrix。

周期不变：
$
\mathcal{D}_i=\left(\mathcal{G}_i^{<}\right)^T \mathcal{R}_i\left(\mathcal{R}_i\right)^T \mathcal{G}_i
$

旋转不变：
$
\tilde{\mathcal{D}}_i=\left(\mathcal{G}_i\right)^T\left(\mathcal{R}_i U\right)\left(\mathcal{R}_i U\right)^T \mathcal{G}_i=\left(\mathcal{G}_i\right)^T \mathcal{R}_i U U^T \mathcal{R}_i \mathcal{G}_i=\mathcal{D}_i
$

神经网络的构建:

数据集构建

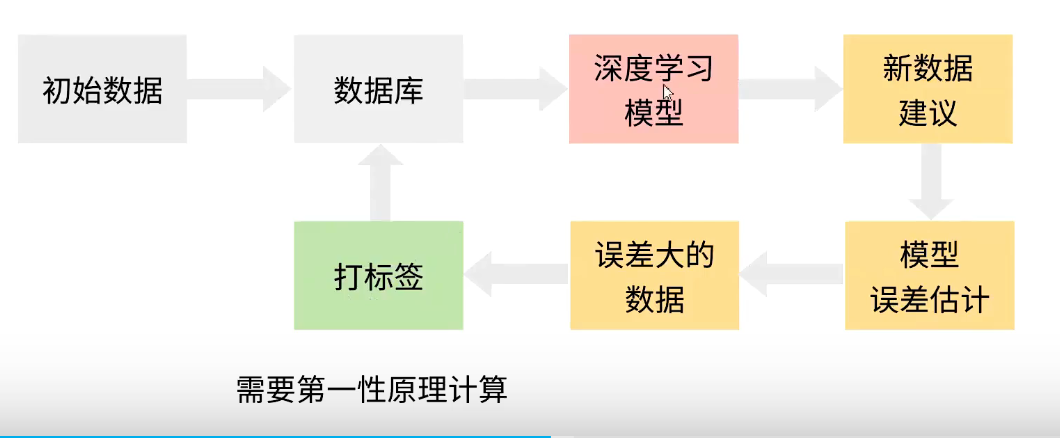
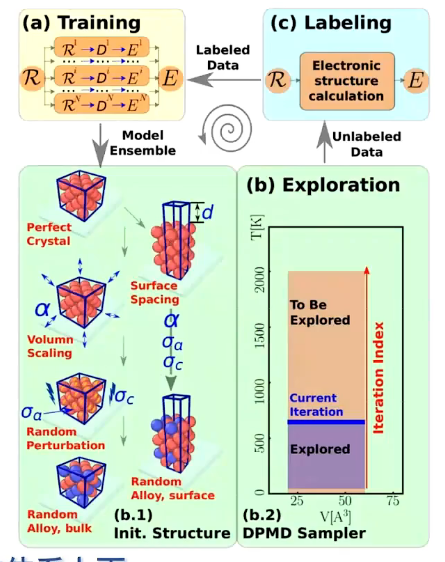
需要保证，大体系结构中的局部体系的结果都在数据集里面有实现。

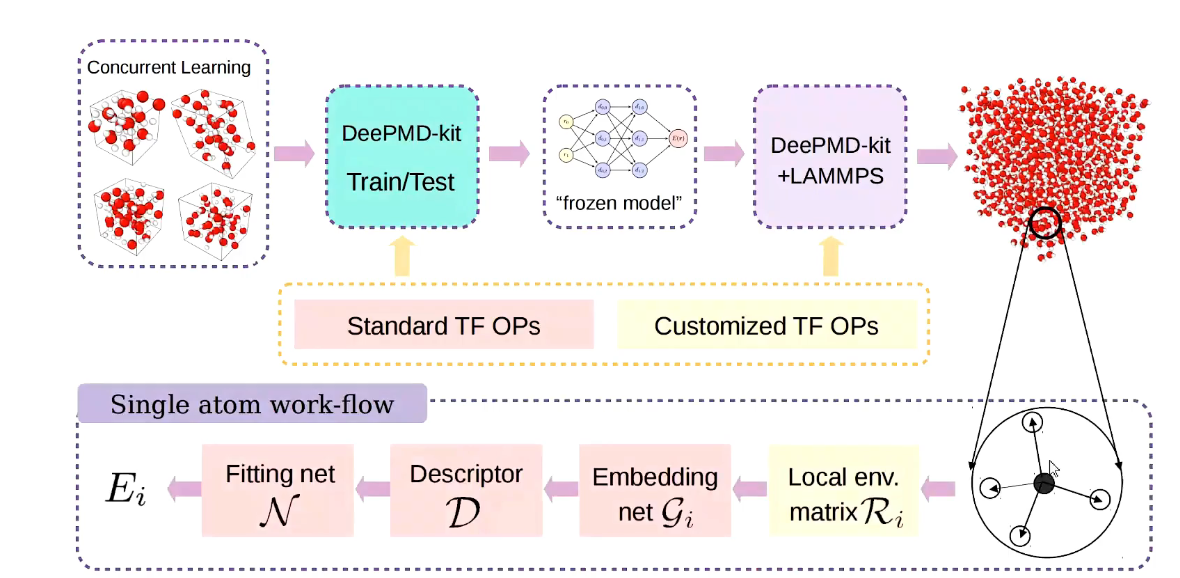
DeePMD-kit 的代码实现

代码修改： DeePMD-kit 的代码实现涉及到几个主要部分，包括trainer，model，embedding net 和 fitting net。trainer 部分解析输入 JSON 文件中的参数。model 部分构建操作图，包括type embed net，embedding net 和 fitting net。embedding net 接收环境矩阵 $ \mathcal{R} $ 作为输入，并输出矩阵 $ \mathcal{G} $。fitting net 接收描述符向量作为输入，并输出能量预测。

模型训练的代码：

class Trainer () :
    def __init__(self, jdata, run_opt):
        # 初始化函数，设置训练参数和运行选项

    def build (self, stop_batch = 0) :
        # 构建训练模型

    def train (self, 
               stop_batch = 0,
               is_init = True, 
               print_iter = 100, 
               save_iter = 1000, 
               save_ckpt = True) :
        # 训练模型的主要函数
        # stop_batch: 停止训练的批次数
        # is_init: 是否初始化模型
        # print_iter: 打印日志的迭代次数
        # save_iter: 保存模型的迭代次数
        # save_ckpt: 是否保存检查点

    def validate (self, 
                  tr_data, 
                  tr_pref) :
        # 验证模型

    def get_feed_dict (self, 
                       batch,
                       is_training) :
        # 获取训练数据的feed字典

    def print_head (self) :
        # 打印训练信息的头部

    def print_info (self, 
                    cur_batch,
                    time,
                    data) :
        # 打印训练信息

训练和验证

使用大量的训练数据（原子配置和相应的能量和力）来训练 DeePMD-kit 模型的神经网络。通过最小化模型预测和实际能量和力之间的差异来调整网络的权重。训练完成后，模型需要使用新数据进行验证，以评估其性能。这涉及将模型在训练期间未见过的原子配置输入，并将模型的预测与实际能量和力进行比较。

模拟

一旦模型经过训练和验证，它就可以用于分子动力学模拟。这是以 Markdown 格式书写的 DeePMD-kit 的概述。这段内容可以粘贴到 Markdown 编辑器或兼容 Markdown 的平台（如 GitHub、Jupyter Notebook等）中，并会被渲染成结构化的文本，包括标题、列表和图片（请注意，图片URL应该被替换为实际的图片链接）。

图神经网络在 DeePMD 中的应用

探讨如何使用图神经网络来改进 DeePMD-kit 的性能和精度。

应用案例

展示 DeePMD-kit 在实际问题中的应用，如材料科学和生物分子。

性能评估

评估 DeePMD-kit 的准确性和效率。

与其他工具的比较

将 DeePMD-kit 与其他分子动力学模拟工具进行比较。

社区和资源

介绍 DeePMD-kit 的社区和相关资源，如文档和教程。

未来展望

探讨 DeePMD-kit 的未来发展方向和潜在改进。

结论

总结报告的主要发现和结论。

参考文献

列出用于编写报告的参考文献。

改进

深度调研DeepMD & 图神经网络。
把图神经网络的思想用进去，要有一些自己的想法。
开学前后。

LOADING