基于原子和神经网络方法的精确和高效的过程模拟
- 作者单位:台积电
这篇论文讨论了一种新的基于机器学习和原子模拟方法的强大研究方法。利用这种方法,作者预测了使用Si2H6(硅烷)前驱体进行硅外延生长的一种先前未被发现的反应序列。这一复杂的表面反应机制通过元动力学模拟揭示出来,它涉及到可控的中间体SiH2的形成过程,解释了在H2载气存在下进行Si2H6吸附时,实验报告中长期未解的生长平台现象。
由于其准确性和灵活的设计,这个工作流模型可以被应用于任何沉积和蚀刻过程条件的优化,以提高薄膜质量,并为下一代电子设备材料提供产量改进的途径。
方法
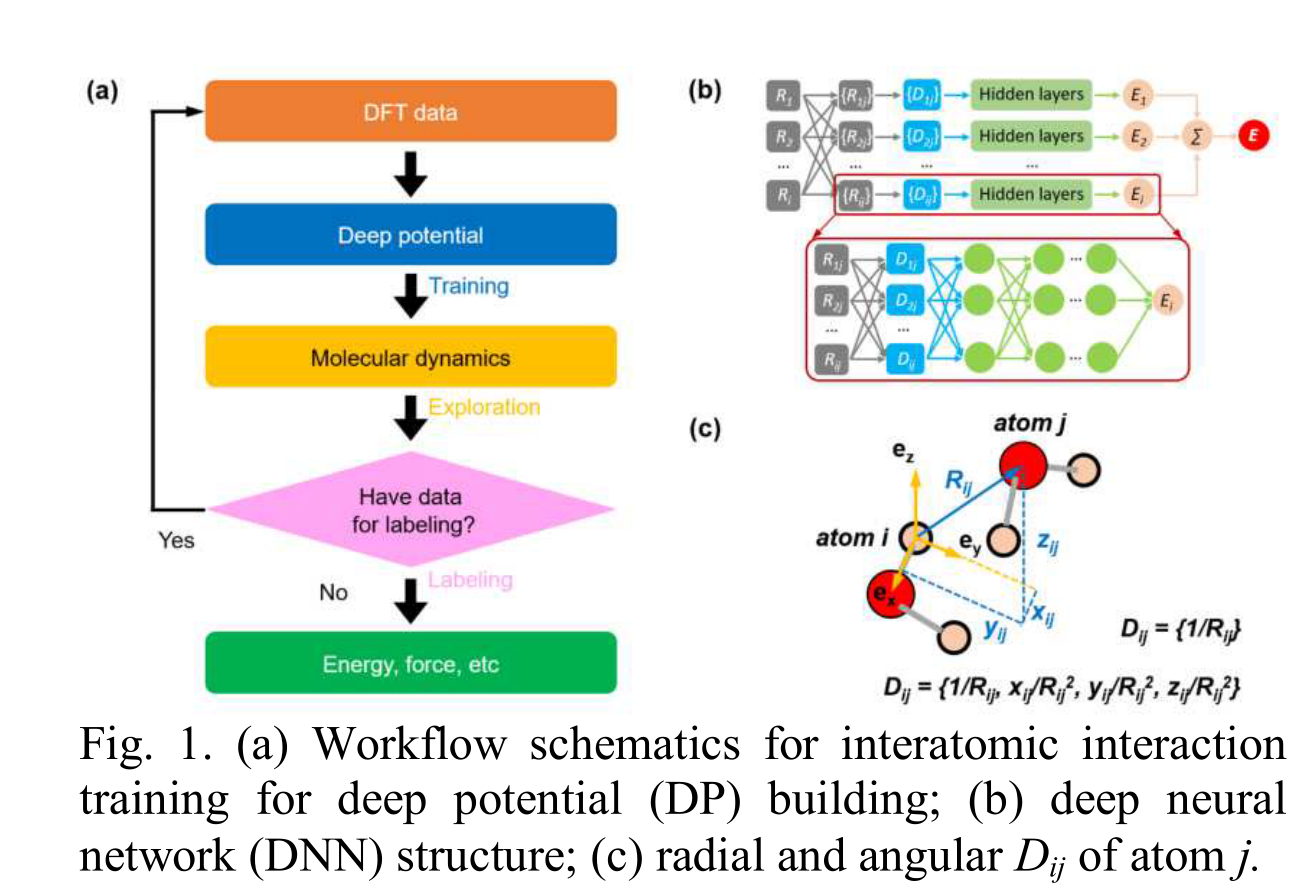
利用VASP和DeepMD来构建深度学习, 就是利用前者计算力场,利用后者拟合。
模型训练与验证
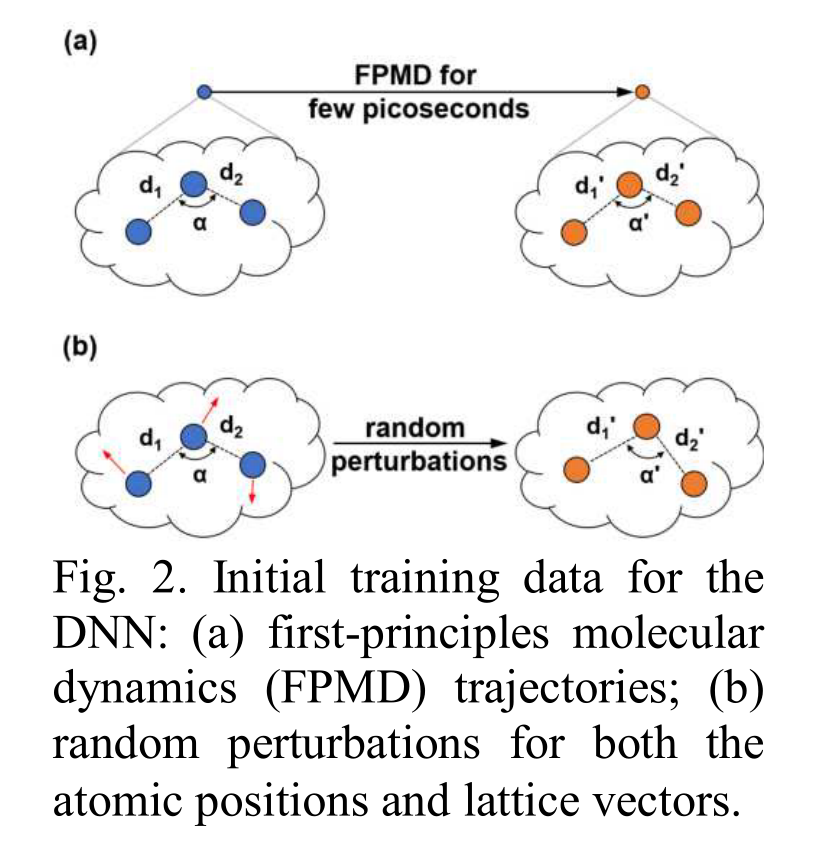
- DNN训练数据生成过程
FPMD
- 生成MD轨迹
DFT
- 对原子位置和晶格向量进行扰动
使用扰动法进行第一个训练周期
主动学习MD方案
- 对大规模、表面和前体吸附配置进行处理
验证
- 跟踪训练中的能量和力的误差
- 对硅的体积电子性质和表面稳定性进行基准测试
- DNN模型基准测试过程
声子特性
- 在声子色散和态密度中捕获关键的声子特性
原子位移演化
- 跟踪顶层原子的原子位移
表面重构
- 进行表面重构
简而言之,利用vasp计算原子模型得到的能量/受力,然后拟合这两者关系得到力场。
VASP计算
定义INCAR(定义计算内容, 类似config,计算能量/受力), POSCAR(给出原子模型)两个文件, 自动生成POTCAR(pseudopotential), 基于此,进行计算, 结果保存在OUTCAR里面。
- INCAR
Collinear Magnetic Calculation
ISPIN = 2 (Spin polarised DFT)
MAGMOM = -4 -4 -4 -4 -4 -4 -4 -4 4 4 4 4 4 4 4 4 4 4 2*4 2*4 2*4 31*0.5 (Set this parameters manually)
LASPH = .TRUE. (Non-spherical elements; d/f convergence)
GGA_COMPAT = .FALSE. (Apply spherical cutoff on gradient field)
VOSKOWN = 1 (Enhances the magnetic moments and the magnetic energies)
LMAXMIX = 4 (For d elements increase LMAXMIX to 4, f: LMAXMIX = 6)
AMIX = 0.2 (Mixing parameter to control SCF convergence)
BMIX = 0.0001 (Mixing parameter to control SCF convergence)
AMIX_MAG = 0.4 (Mixing parameter to control SCF convergence)
BMIX_MAG = 0.0001 (Mixing parameter to control SCF convergence)
DFT+U Calculation
LDAU = .TRUE. (Activate DFT+U)
LDATYPE= 2 (Dudarev; only U-J matters)
LDAUL = 2 2 2 2 -1 (Orbitals for each species)
LDAUU = 4 4 4 4 0 (U for each species)
LDAUJ = 0.5 0.5 0.5 0.5 0 (J for each species)
LMAXMIX= 4 (Mixing cut-off; 4-d, 6-f)
Global Parameters
ISTART = 1 (Read existing wavefunction; if there)
# ISPIN = 2 (Spin polarised DFT)
# ICHARG = 11 (Non-self-consistent: GGA/LDA band structures)
LREAL = Auto (Projection operators: automatic)
ENCUT = 600 (Cut-off energy for plane wave basis set, in eV)
PREC = Normal (Precision level)
LWAVE = .TRUE. (Write WAVECAR or not)
LCHARG = .TRUE. (Write CHGCAR or not)
ADDGRID= .TRUE. (Increase grid; helps GGA convergence)
# LVTOT = .TRUE. (Write total electrostatic potential into LOCPOT or not)
# LVHAR = .TRUE. (Write ionic + Hartree electrostatic potential into LOCPOT or not)
# NELECT = (No. of electrons: charged cells; be careful)
# LPLANE = .TRUE. (Real space distribution; supercells)
# NPAR = 4 (Max is no. nodes; don't set for hybrids)
# NWRITE = 2 (Medium-level output)
# KPAR = 2 (Divides k-grid into separate groups)
# NGX = 500 (FFT grid mesh density for nice charge/potential plots)
# NGY = 500 (FFT grid mesh density for nice charge/potential plots)
# NGZ = 500 (FFT grid mesh density for nice charge/potential plots)
Electronic Relaxation
ISMEAR = 0 (Gaussian smearing; metals:1)
SIGMA = 0.05 (Smearing value in eV; metals:0.2)
NELM = 200 (Max electronic SCF steps)
#NELMIN = 6 (Min electronic SCF steps)
EDIFF = 1E-04 (SCF energy convergence; in eV)
# GGA = PS (PBEsol exchange-correlation)
Ionic Relaxation
NSW = 200 (Max ionic steps)
IBRION = 2 (Algorithm: 0-MD; 1-Quasi-New; 2-CG)
ISIF = 2 (Stress/relaxation: 2-Ions, 3-Shape/Ions/V, 4-Shape/Ions)
EDIFFG = -5E-02 (Ionic convergence; eV/AA)
Other Sets
#ISYM = 0
LORIBT = 11
LREAL = auto
LDIPOL = .TRUE.
IDIPOL = 3
- POSCAR
result1\(-1\0\0)\(2)
1.00000000000000
8.4650001526000000 0.0000000000000000 0.0000000000000000
0.0000000000000000 8.4650001526000000 0.0000000000000000
0.0000000000000000 0.0000000000000000 22.4559993744000010
Fe Mn Co Ni O
18 2 2 2 31
Selective dynamics
Direct
0.91149922 0.93394451 0.30298449 T T T
0.54928124 0.56044684 0.29732690 T T T
0.00078665 0.50685843 0.14280074 T T T
0.50100867 -0.00087781 0.14336777 T T T
0.74966002 0.24499001 0.04966000 F F F
0.25306246 0.24622419 0.24308685 T T T
0.75646493 0.73886826 0.23682094 T T T
0.24959000 0.74254000 0.04955000 F F F
0.36362551 0.88939961 0.28422896 T T T
0.37275001 0.37446999 0.09679000 F F F
0.62655997 0.87489003 0.00145000 F F F
0.88892126 0.37871634 0.27967138 T T T
0.12474000 0.37724000 0.00286000 F F F
0.13537451 0.87019407 0.19315328 T T T
0.87775999 0.87234002 0.09593000 F F F
0.61822538 0.36499678 0.19073725 T T T
0.37485999 0.12455000 0.00229000 F F F
0.12609001 0.12396000 0.09679000 F F F
0.87503127 0.12539944 0.19149679 T T T
0.62344003 0.62557000 0.09738000 F F F
0.87712997 0.62597001 0.00195000 F F F
0.61720147 0.11961980 0.28503860 T T T
0.36775063 0.62527783 0.19060239 T T T
0.11978615 0.61702653 0.28201958 T T T
0.38083549 0.37785134 0.19095691 T T T
0.88235998 0.11405000 0.09627000 F F F
0.66019525 0.87924509 0.29268959 T T T
0.12107000 0.61469001 0.00023000 F F F
0.35538812 0.65701680 0.28963690 T T T
0.86782998 0.87575001 0.00517000 F F F
0.13143000 0.37704000 0.09430000 F F F
0.62352750 0.13241024 0.19208011 T T T
0.36914000 0.13489001 0.09718000 F F F
0.12902930 0.63325776 0.19266269 T T T
0.87686175 0.60810064 0.28978881 T T T
0.11830000 0.87140000 0.09951000 F F F
0.61862999 0.11504000 0.00147000 F F F
0.88683371 0.87465383 0.18953353 T T T
0.37419000 0.61343998 0.09935000 F F F
0.11465552 0.38072686 0.28473890 T T T
0.85682220 0.15173567 0.29227789 T T T
0.36780000 0.37867001 0.00566000 F F F
0.63459998 0.87900001 0.09384000 F F F
0.87550002 0.63556999 0.09510000 F F F
0.11433896 0.85777596 0.28410816 T T T
0.38352337 0.11589898 0.28979767 T T T
0.61631000 0.37123001 0.10025000 F F F
0.88268000 0.37531999 0.00032000 F F F
0.61149357 0.60937161 0.19422251 T T T
0.36969135 0.86804908 0.18981720 T T T
0.13167000 0.13587000 0.00198000 F F F
0.63001001 0.63647002 0.00231000 F F F
0.12931348 0.11474703 0.18829403 T T T
0.38371000 0.87102997 0.00000000 F F F
0.86592531 0.37820479 0.19126102 T T T
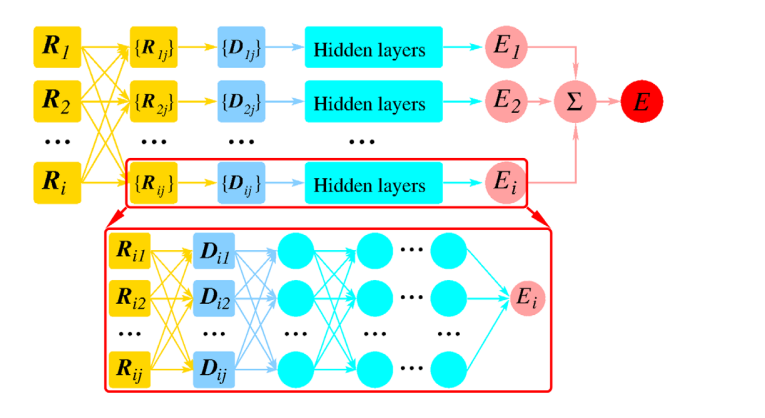
DeepMD计算
- 原理
- 原子的能量可以有临近的环境决定(截断半径$R_c$的大小。)
$$
E = \sum_{i} E_{i}
$$
- $E_i$ 的构建步骤:
- 首先构造一个新的坐标系用于保持环境的平移、旋转和置换对称:
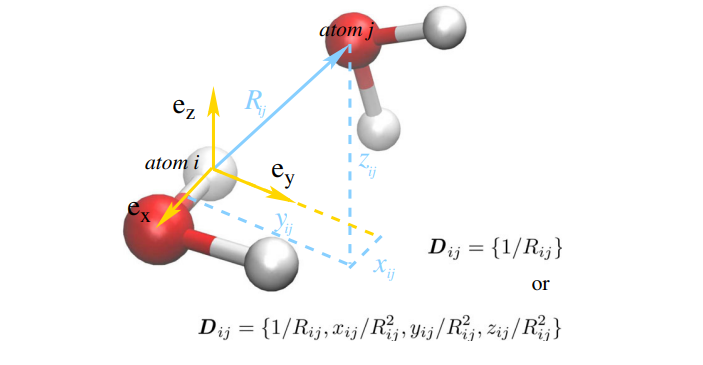
- 新坐标系的$D_{ij}$ 作为DNN神经网络的输入用于求解$E_i$, 这里采用的是
MLP神经网络
- 基于
Adam优化算法来进行优化, 定义损失函数如下:
$$
L\left(p_\epsilon, p_f, p_{\xi}\right)=p_\epsilon \Delta \epsilon^2+\frac{p_f}{3 N} \sum_i\left|\Delta \boldsymbol{F}i\right|^2+\frac{p{\xi}}{9}|\Delta \xi|^2
$$
$\Delta$:这个表示DPMD(Deep Potential Molecular Dynamics)预测与训练数据之间的差异。这个差异可能会被用来计算模型的损失函数,以便在训练过程中调整模型的参数。
$N$:这个表示原子的数量。在物理和化学的模拟中,这个参数通常用来表示系统的大小或复杂性。
$\epsilon$:这个表示每个原子的能量。在物理和化学的模拟中,这个参数通常用来表示系统的总能量或者能量分布。
$\boldsymbol{F}_i$:这个表示作用在第$i$个原子上的力。在分子动力学模拟中,这个参数通常用来计算原子的运动。
$\xi$:这个表示单位原子的”virial tensor”(或称为”维里张量”),它定义为$\Xi=-\frac{1}{2} \sum_i \boldsymbol{R}_i \otimes \boldsymbol{F}_i$,然后除以原子的数量$N$。维里张量是一个描述系统压力和体积变化关系的物理量。
$p_\epsilon, p_f$, 和 $p_{\xi}$:这些是可调的预因子(prefactors),它们可以在训练过程中调整,以达到最小化损失函数的目标。当数据中缺少virial信息时,我们设定$p_{\xi}=0$。在训练过程中,我们逐渐增大$p_\epsilon$和$p_{\xi}$,同时减小$p_f$,以确保在训练开始时,力的项占主导,而在训练结束时,能量和virial项变得重要。
基于前面VASP 计算得到的数据,便可以开始训练力场了。

之前配置的内容:
{
"model": {
"type_map": ["Ca","Si","O","H"],
"descriptor" :{
"type": "se_a",
"sel": [30,30,90,70],
"rcut_smth": 6.80,
"rcut": 7.00,
"neuron": [25, 50, 100],
"resnet_dt": false,
"axis_neuron": 16,
"seed": 1
},
"fitting_net" : {
"neuron": [40,40,40],
"resnet_dt": true,
"coord_norm": true,
"type_fitting_net": false,
"seed": 1
}
},
"loss": {
"start_pref_e": 0.02,
"limit_pref_e": 1,
"start_pref_f": 1000,
"limit_pref_f": 1,
"start_pref_v": 0,
"limit_pref_v": 0
},
"learning_rate": {
"type": "exp",
"decay_steps": 5000,
"start_lr": 0.001,
"stop_lr": 3.51e-9
},
"training": {
"systems": [数据集路径],
"set_prefix": "set",
"stop_batch": 500000,
"batch_size": 1,
"seed": 1,
"_comment": "frequencies counted in batch",
"disp_file": "lcurve.out",
"disp_freq": 100,
"numb_test": 50,
"save_freq": 1000,
"save_ckpt": "model.ckpt",
"load_ckpt": "model.ckpt",
"disp_training": true,
"time_training": true,
"profiling": false,
"profiling_file": "timeline.json"
}
}


结果讨论
- SiH$_4$和Si$_2$H$_6$吸附的反应动力学。
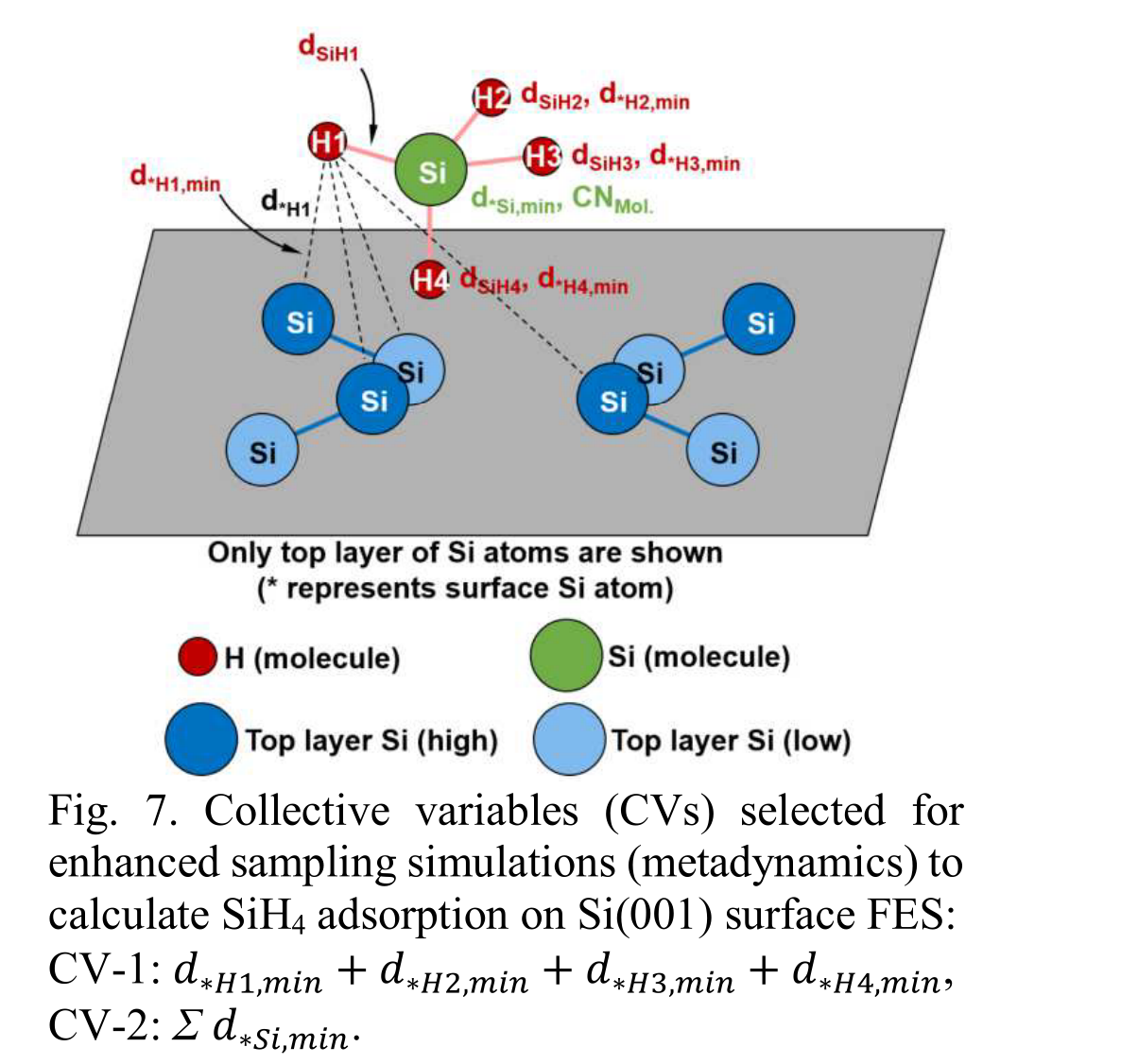
- 自由能表面(FES)计算:该表面描述了化学反应的空间。它是通过使用元动力学模拟和增强采样方法来计算的。元动力学模拟是一种计算方法,可以帮助研究者对复杂系统的自由能表面进行建模和分析。
- 高斯山(Gaussian hills):整个势能表面是通过随机添加潜在能量(“高斯山”)来采样的。高斯山是元动力学模拟中的一个重要概念,用于改变势能表面,以提高探索率并避免陷入局部最小值。
- 集体变量(CVs)选择:选择集体变量是一个关键的决策步骤,它需要确保对整个前体吸附过程的准确和有效的物理预测。集体变量是元动力学模拟中的一个重要概念,它表示系统中重要的、可变的参数。
- SiH4吸附:文本描述了SiH4吸附过程中的关键反应中间体和激活能。这些结果与之前的模拟结果相符。
- Si2H6吸附:在温度低于700K时,Si2H6吸附的速率限制步骤是第一个反应*H + Si2H5,其中一个氢被转移到表面,激活能为0.34 eV。
- Si2H6气相分解:在温度高于700K时,Si2H6的分解过程包括生成SiH2和SiH4的中间产品以及Si2H4和H2气体,它们的激活能都约为2 eV。实验表明,SiH2产品容易在36.5 Torr和720 K的条件下在表面上吸附。
硅生长的新反应机制揭示
氢脱附的可能的其他的反应途径
- 氢解吸的替代反应路径:这个替代反应路径在图10中以示意图的形式描绘。解吸是吸附过程的逆过程,也就是说,吸附到物质表面的粒子离开表面并回到气相。
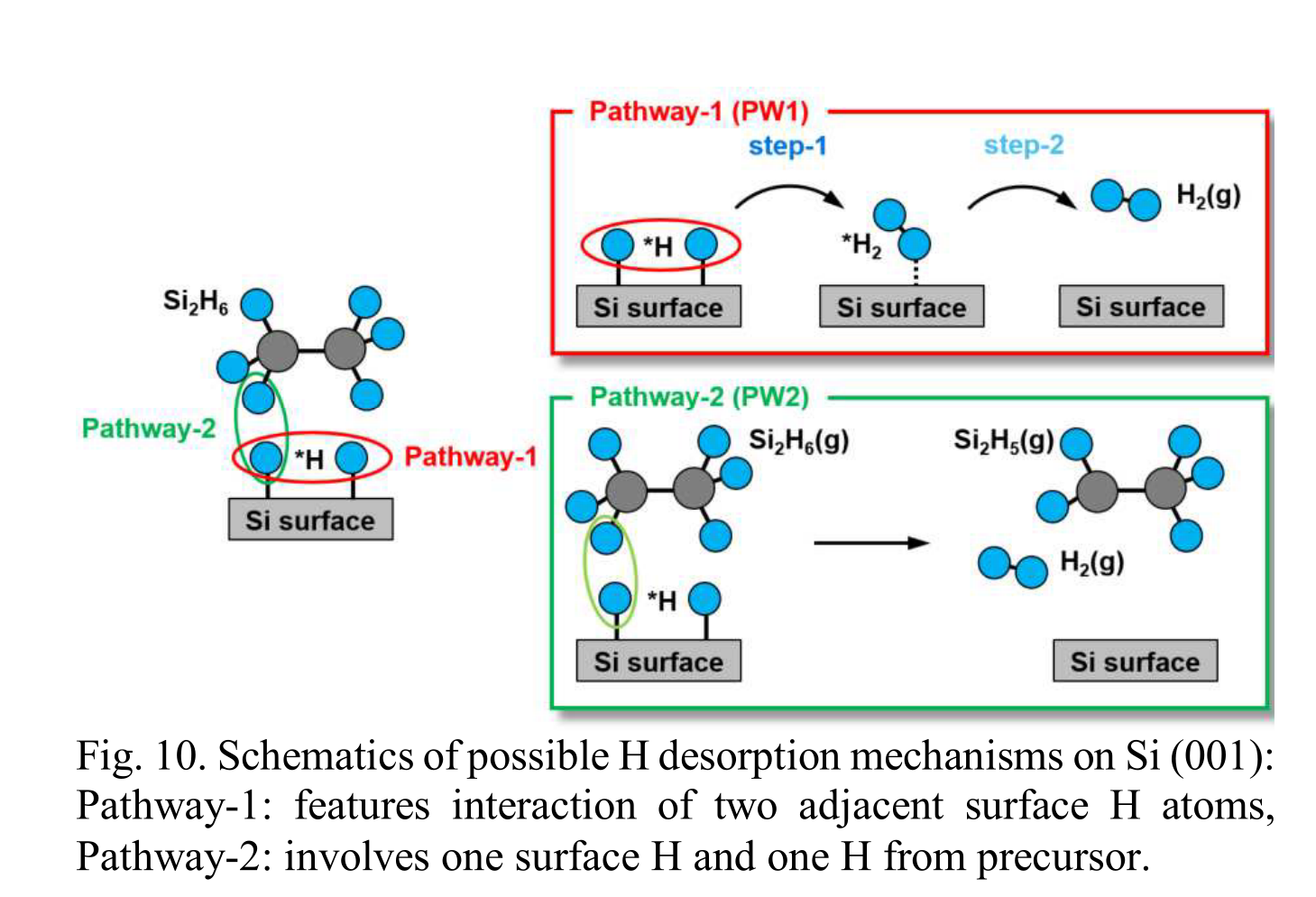
- 文献中的氢解吸路径:通常文献中讨论的氢解吸路径涉及到两个表面氢(surface H)。表面氢是指已经吸附在物质表面上的氢原子。
- 表面氢和前驱体氢的相互作用:然而,表面氢与前驱体氢的相互作用产生了更低的活化能。这个过程在图11中展示。活化能是一种反应需要的能量,更低的活化能意味着反应更容易进行。
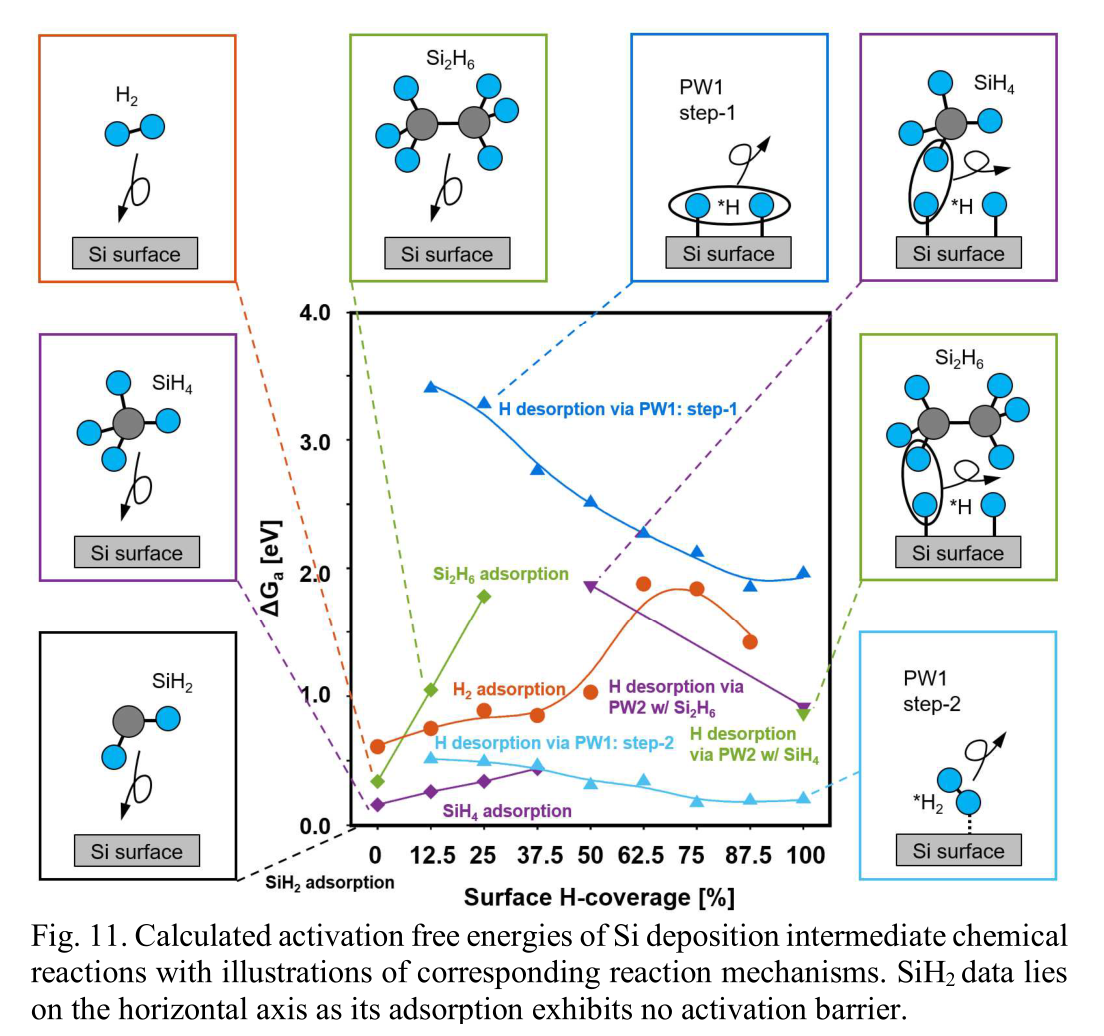
- 影响因素:当前驱体或载气流量增加时,这个具有较低活化能的过程可能更容易发生。这意味着,通过改变前驱体或载气的流量,可以影响这个反应过程。
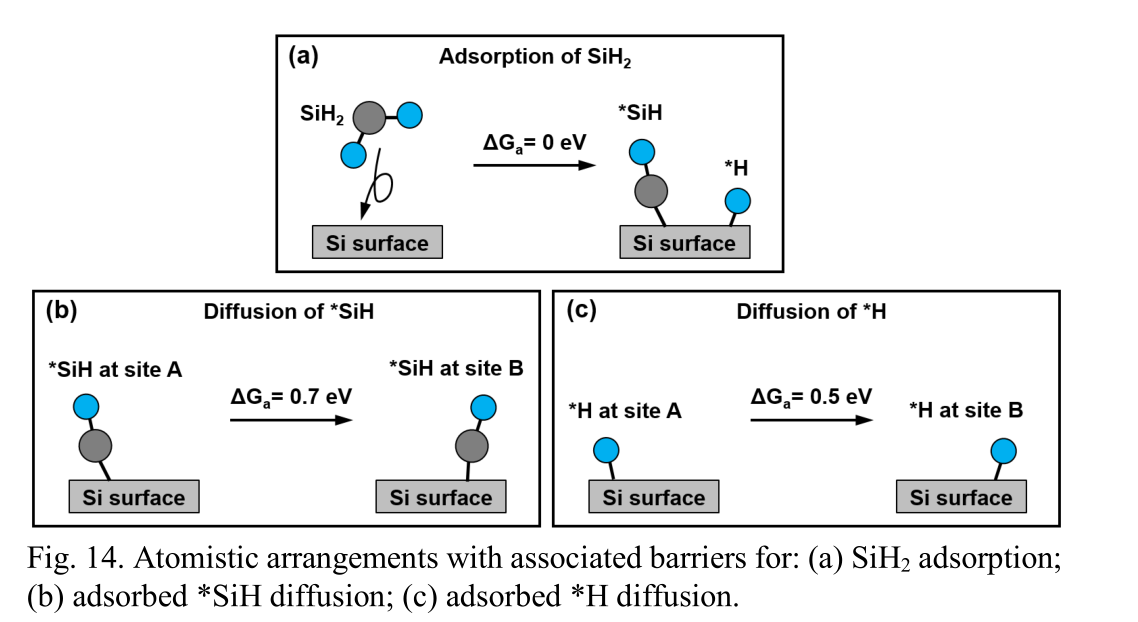
分解产物SiH2的吸附
- SiH2的吸附:通过DPMD研究预测,SiH2可以在无阻力的过程中自发地吸附在Si表面(图9,公式4)。当活化能Ea= 0 eV时,根据阿伦尼乌斯方程,SiH2在大于700 K的温度范围内的吸附速度是常数,这导致生长速率呈现出一个平台阶段。

- Si的生长过程:为了全面了解从低温到高温的Si生长过程,计算了所有可能的表面反应作为表面氢覆盖率的函数(图11)。反应速率在SiH4、Si2H6和SiH2吸附,H2吸附和所有已知H解吸路径中被提取出来(图12)。由于SiH2的吸附没有活化障碍,其数据被放置在水平轴上。
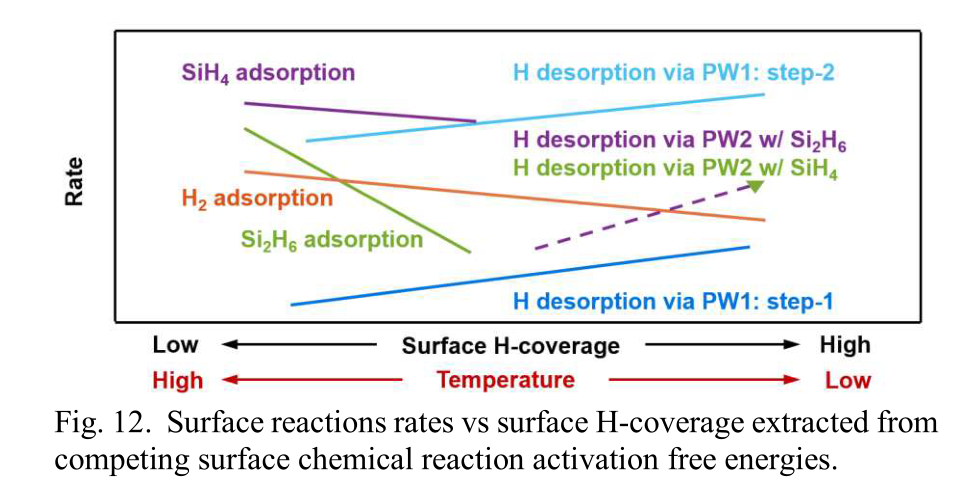
- Si生长的模拟:模拟了通过Si2H6沉积生长Si的过程,这也支持了之前提出的在低温和高温区间存在明显分界线的观点(图13)。在低温区,根据图11和图12,H的解吸被证实为速率限制步骤。当温度适度增加时,H表面覆盖率略有降低,而可供前驱体吸附的Si表面积增加,因此Si的生长速率随温度的升高而增加。
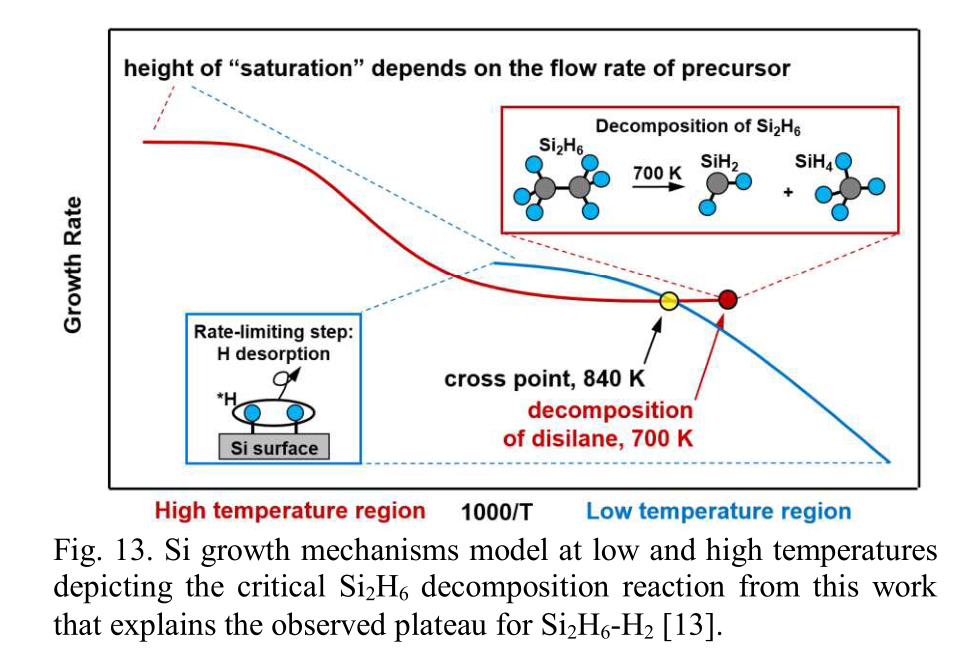
- 高温区的特性:在约700 K,Si2H6在气相中开始分解,生成SiH2和SiH4。因为SiH2在Si表面的吸附是无阻力的过程,所以它在中温和高温区域占主导,引起了生长速率的“恒定”并定义了低温和高温机制之间的“交叉点”(图13)。此外,SiH2吸附产生表面SiH键,SiH(0.7 eV)或H(0.5 eV)的小表面扩散障碍在大于700 K可热力学上实现,促进了表面重排和加速了H2的解吸(图14)。
- 更高温度下的行为:在大约840 K的高温开始,表面H覆盖率显著降低,任何前驱体或产品(SiH4,Si2H6,或SiH2)都可以直接在表面沉积,直到约1100 K生长速率“饱和”,系统进入由前驱体流速限制的阶段。
总体研究步骤
建立反应模型:研究者首先定义了一个包含SiH4等分子的系统。这个系统可能包括了所有可能的反应参与者和环境条件。
拟合势能面:DeepMD是一种基于深度学习的势能面拟合方法。这个模型使用一组从量子力学计算得到的数据作为训练集,这些数据可能包括原子间的距离、角度、能量等信息。DeepMD模型通过训练学习这些数据的特征,拟合出整个反应系统的势能面。在拟合过程中,DeepMD模型能够学习到各种原子间的相互作用,从而精确地模拟复杂的反应过程。
搜索反应路径:在得到势能面后,研究者就可以在这个势能面上搜索反应路径。这通常是通过启动分子动力学模拟来完成的。模拟过程中,系统会在势能面上进行演化,寻找从反应物到产物的最低能量路径。这个过程可以揭示反应的过渡态(Transition State),也就是反应路径上的能量最大点。
力场(势能面)的建立:在量子力学级别上进行高精度的力场参数化,使用深度学习算法(如DeepMD)训练并拟合出描述分子内部和分子间相互作用的势能面。这个过程需要大量的量子力学计算数据,包括不同原子构型下的能量、力等。经过训练,DeepMD模型将能够对新的原子构型给出相应的势能和力的预测。
分子动力学模拟:利用上一步拟合得到的势能面(力场),进行分子动力学模拟。这个过程中,分子在力场的驱动下进行运动,经过一段时间后,可以获得反应的动态过程。通过分析模拟得到的轨迹,可以找到反应的过渡态、中间产物,以及反应速率等信息,从而揭示反应的详细机理。
揭示反应机理:通过对反应路径的分析,研究者可以揭示反应的详细机理。这可能包括反应的中间态、过渡态以及反应的速率常数等信息。例如,SiH4分子在反应过程中可能会经历一系列的断裂和形成,通过分析这些信息,研究者可以得出SiH4分子在反应过程中的详细行为,从而了解其反应机理。
